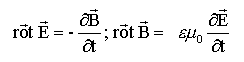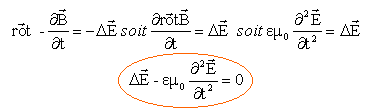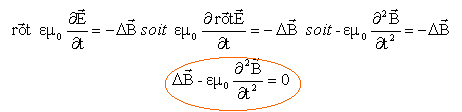|
|
||
|
||
|
Une onde électromagnétique polarisée se propage suivant un axe Oz. Elle arrive sous incidence normale à la surface de séparation de deux diélectriques d'indice n1 et n2.
Les vecteurs sont écrits en bleu et en gras. Une onde est polarisée rectilignement lorsque les champs E et B gardent une direction déterminée au cours de la propagation. Une onde électromagnétique dans un milieu linéaire, homogène et isotrope est caractérisée par 4 vecteurs : E, D (vecteur induction électrique) , B et H (vecteur excitation magnétique). D = e E avec e permittivité absolue du milieu. B = m H avec m perméabilité magnétique absolue du milieu. m voisin de m0 si le milieu n'est pas ferromagnétique donc : B = m0 H dans les milieux diélectriques parfaits la conductivité g est nulle et J =g E = 0. les équations de Maxwel s'écrivent alors : div D = r (nul s'il n'y ni charge, ni courant de conduction) div B = 0 ; équation de propagation du champ électrique : formons : rot rot E = grad div E - DE. or div E =0 ( s'il n'y ni charge, ni courant de conduction)
équation de propagation du champ magnétique : formons : rot rot B = grad div B - DB. or div B =0
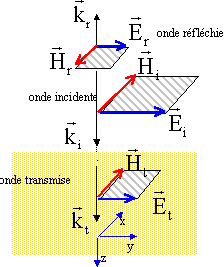
réflexion et réfraction normale : Soit une surface plane (p) séparant deux milieux isolants de permitivités e 1 et e 2 de perméabilité magnétique m1 et m2 voisin m0. Soit une onde électromagnétique incidente (Ei, Hi )à laquelle correspondent une onde réfractée (transmise) (Er, Hr) et une onde réfléchie (Et, Ht).
à l'interface des deux milieux d'indice n1 et n2 : on note Ei m , Er m et Et m les amplitudes des champs Ei, Er, Et, v1 et v2 les célérités de l'onde dans les milieux 1 et 2. on note Hi m , Hr m et Ht m les amplitudes des champs Hi, Hr, Ht. écrire la continuité de la composante tangentielle de E : Ei m + Er m = Et m (1) écrire la continuité de la composante tangentielle de H : Hi m - Hr m = Ht m avec Hi m = Ei m / v1. d'où : Ei m / v1-Er m / v1= Et m / v2. (2) (1)/ v2 -(2) s'écrit : Ei m (1/ v2-1/ v1)+ Er m (1/ v2+1/ v1) =0 or n1= c /v1 et n2= c /v2 d'où Ei m (n2- n1)+ Er m ( n2+ n1) =0 d'où le facteur de réflexion en amplitude r = Er m / Ei m = (n1- n2) / ( n2+n1). r est positif si n1 est supérieur à n2. r est négatif si n1 est inférieur à n2 ce qui se traduit par un déphasage de p de l'onde réfléchie. (1)/ v1 +(2) s'écrit : Ei m (1/ v1+1/ v1)= Et m (1/ v2+1/ v1) Ei m (n1+ n1)= Et m (n2+n1) d'où le facteur de transmission en amplitude t = Et m / Ei m = 2n1 / ( n2+n1). pouvoir réflecteur R et pouvoir de transmission T : R = n1 E²rm / (n1 E²i m) = r² = (n1- n2)² / ( n2+n1)². T = n2 E²t m / (n1 E²i m) = n2 / n1 t² = 4 n2 n1/ ( n2+n1)². on vérifie qu'il y a conservation de l'énergie car R+T =1. application numérique : n1 =1 et n2 = 1,5 : R = 0,5² / 2,5² = 0,04 T = 4*1*1,5 / 2,5² = 0,96. |