u = ½ e₀ E² + ½ B² / m₀

or B = E / c d'où : u = ½ e₀ E² + ½ E² / (m₀ c²)

or e₀ m₀ c²=1 d'où : u = ½ e₀ E² + ½ e₀ E² = e₀ E².

les deux termes qui composent u sont égaux : équipartition de l'énergie.

valeur moyenne de l'énergie :

E= E₀ cos(wt-kx)

<u>=e₀ E₀² <cos²(wt-kx) >

or la valeur moyenne du terme en cos² est ½ sur une période

d'où : <u>= ½e₀ E₀²

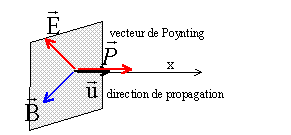
les grandeurs écrites en bleu et en gras sont des vecteurs

P = E^B / m₀ avec B = u^ E /c et E = cB^ u

d'où : P = cB²/ m₀ u = ce₀ E² u.

l'énergie se propage dans le sens de l'onde à la vitesse c.

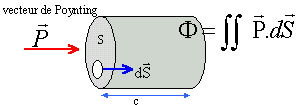
F = PS=ce₀ E²S

valeur moyenne <F> =ce₀ S <E² >= ½ ce₀ S E₀².

La norme du vecteur de Poynting varie très rapidement et le détecteurs ne peuvent pas suivre instantanément. Ils donnent une valeur moyenne sur une durée de réponse très supérieure à la période de l'onde.

superposition d'une onde incidente et d'une onde réfléchie.

E ( E_x=0 ; E_y = -2 E₀ sin(wt) sin(kx) ; E_z =0)

B ( B_x=0 ; B_y = 0 ; B_z =-2 /c E₀ cos(wt) cos(kx) )

on a le produit d'une fonction d'espace et d'une fonction du temps: il ne s'agit donc pas d'une onde qui se propage mais d'une onde stationnaire. Les amplitudes de E et B ne dépendent que de x.

noeuds de E ( amplitude nulle) : sin(kx) =0 soit x = np/k =½nl.

ventres de E ( amplitude maxi) : sin(kx) =1 soit x = np/k+½p/k =½nl+l/4

noeuds de B ( amplitude nulle) : cos(kx) =0 soit x = np/k+½p/k =½nl+l/4

coïncident avec les ventres de E.

ventres de B ( amplitude maxi) : cos(kx) =1 soit x =np/k =½nl

coïncident avec les noeuds de E.

u = ½ e₀ E² + ½ B² / m₀

u = ½e₀ 4 E₀² sin²(wt) sin²(kx) + ½ / (m₀ c²) 4 E₀² cos²(wt) cos²(kx)

or e₀ m₀ c²=1 d'où : u = 2 e₀ E₀² (sin²(wt) sin²(kx) + cos²(wt) cos²(kx))

les deux termes qui composent u sont inégaux : il n'y a plus équipartition de l'énergie.

il passe à travers une surface S, le même flux d'énergie dans les deux sens opposés (onde incidente et réléchie) :

le bilan vectoriel est nul

l'énergie est confinée entre les noeuds distants de l /4.

valeur moyenne de l'énergie :

<u>=2 e₀ E₀² <(sin²(wt) sin²(kx) + cos²(wt) cos²(kx)) >

la valeur moyenne de sin²(wt) et de cos²(wt) est ½

<u>=2 e₀ E₀² (½ sin²(kx) + ½ cos²(kx))

<u>=e₀ E₀² (sin²(kx) + cos²(kx)) = e₀ E₀².

vecteur de Poynting :

P = E^B / m₀ = 4E₀²/ (m₀c)sin(wt) sin(kx) cos(wt) cos(kx) u_x.

d'où : P = E₀²/ (m₀c)sin(2wt) sin(2kx)

valeur moyenne de ce vecteur :

<P > =E₀²/ (m₀c) <sin(2wt) sin(2kx)> =0

pas de propagation d'énergie.

retour - menu