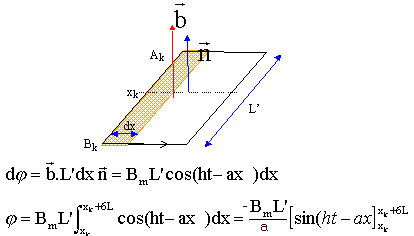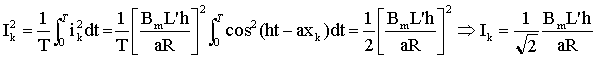Aurélie 02/02
réseau électrique ayant la forme d'une échelle

Google

 

Les vecteurs sont écrits en bleu et en gras.

Un réseau électrique a la forme d'une échelle indéformable. Ce réseau est plongé dans un champ magnétique b fonction du temps et de l'abscisse x : b = Bm cos( ht-ax) u3 avec h (rad/s), a (m-1) et Bm constants. Des courants sont induits dans l'échelle ; il s'agit de calculer la force électromagnétique F qui s'exerce sur l'échelle.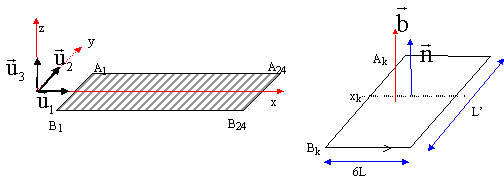

Les barreaux sont des conducteurs AkBk de longueur L', distants de L, de résistance R. Les montants sont de résistance nulle. On choisit le circuit rectangulaire AkBkBk+6Ak+6 désigné Ck. Il limite une surface Sk. On choisit un sens de parcours de ce circuit. Le courant induit dans Ck est le même que si Ck existait seul. La longueur L (m) est telle que 6aL =p.

  1. Calculer le flux magnétique j (t,xk) à travers Sk en fonction de t, L', Bm, h, a xk.
  2. En déduire la valeur instantanée du courant induit i (t,xk).
  3. Quelle est en fonction de L', Bm, h, a et R la valeur efficace Ik de ce courant ?
  4. Chaque conducteur AkBk est soumis à une force électromagnétique parallèle à Ox. Préciser sur une figure de Ck, à un instant où b(t, xk) est positif, le sens du courant induit ik et les forces électromagnétiques qui s'exercent sur les conducteurs AkBket Bk+6Ak+6.
  5. La force Fk qui s'exerce sur Ck est Fk = Fk u1. Exprimer Fk en fonction de t et xk, et Bm,a, h, L' et R.
  6. Calculer la valeur moyenne de Fk en fonction de Bm,a, h, L' et R.
  7. Le calcul montrerait que la force électromagnétique totale F qui s'exerce sur l'échelle est indépendante du temps . Déterminer F.
 

corrigé
flux à travers Sk :

chercher le flux élémentaire du champ à travers la surface élémentaite dS = L'dx puis intégrer entre xk et xk+6L.

j = -BmL' / a [sin (ht -axk-6aL)-sin (ht -axk) ]

or sin a -sin b = 2 cos ((a+b)/2) sin ((a-b)/2)

avec ½(a+b) = ht-axk-3aL = ht-axk -½p.

avec ½(a-b) = -6aL = -½p.

j = -2BmL' / a cos (ht-axk -½p) sin (-½p) avec cos (x-½p) = sin x

j = 2BmL' / a sin (ht-axk ).

force électromotrice :

ek = - dj/ dt = -2BmL' h / a cos (ht-axk)

courant induit : i k = ek/ (2R), la résistance du circuit Ck étant 2R

i k = -BmL' h / (aR) cos (ht-axk)

si cos ((ht-axk) positif soit b dirigé vers le haut en xk , le courant induit ik a le sens contraire au sens choisi du parcours Ck.

valeur efficace de ik :

calculer la primitive de i²k sur une période en remarquant que l'intégrale de cos ²(ht-axk) vaut ½ sur une période.

la valeur efficace d'un courant sinusoïdal est égale à l'amplitude divisée par racine carrée de 2.

force électromagnétique :

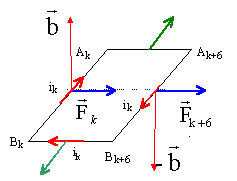
sur l'élément AkBk : Fk = ik L' (u2)^ b = ik L' Bmcos (ht-axk) (u1)

Fk =  (BmL' )² h / (aR) cos² (ht-axk)(u1)

sur l'élément Bk+6Ak+6 :

remarquons que Bmcos (ht-axk-6aL) = Bm cos (ht-axk-p) = -Bmcos (ht-axk)

le champ a le sens contraire à celui qu'il avait en xk et le courant a également le sens contraire à celui qu'il avait en xk, donc Fk etFk+6 ont le même sens.

Fk+6 = ik L' (-u2)^ b = ik L' Bmcos (ht-axk-6aL) u1.

Fk+6 =  (BmL' )² h / (aR) cos (ht-axk)cos (ht-axk-6aL)u1 or 6aL = p.

Fk+6 =  (BmL' )² h / (aR) cos (ht-axk)cos (ht-axk-p) u1 ; or cos (x -p) = - cos x

Fk+6 =  (BmL' )² h / (aR) cos² (ht-axk)( -u1).

sur les éléments BkBk+6 et Ak+6Ak les forces sont opposées.

Fk +Fk+6 = 2Fk = 2 (BmL' )² h / (aR) cos² (ht-axk) (u1).

valeur moyenne de cette force électromagnétique :

<force> = 2 (BmL' )² h / (aR) <cos²(ht-axk) >

la valeur moyenne de cos ²(ht-axk) est égale à ½

<force>= (BmL' )² h / (aR).

force électromagnétique sur tout le circuit :

addition vectorielle des forces s'exerçant sur chaque circuit Ck avec k variant de 1 à 18.

circuit
force
A1B1B7A7 désigné C1.
2 (BmL' )² h / (aR) cos² (ht-ax1) u1.
A2B2B8A8 désigné C2.
2 (BmL' )² h / (aR) cos² (ht-ax1- p/6) u1.
A3B3B9A9 désigné C3.
2 (BmL' )² h / (aR) cos² (ht-ax1- 2p/6) u1.
AkBkBk+6Ak+6 désigné Ck.
2 (BmL' )² h / (aR) cos² (ht-ax1- (k-1)p/6) u1.

retour - menu