|
|
||
|
||
|
Dans un solénoïde très long, d'axe Oz, comptant n spires par mètre, on place un barreau cylindrique métallique de longueur h et de rayon R, dont l'axe est confondu avec celui du solénoïde. Un courant i = i0 cos (wt) traverse le solénoïde. On travaillera avec les coordonnées cylindriques. La conductivité du conducteur est notée g. Les grandeurs écrites en bleu et en gras sont des vecteurs. 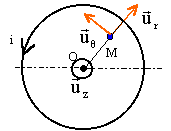
le conducteur cylindrique est placé dans un champ magnétique B variable au cours du temps : il apparaît un champ électrique Em et des courants dans le conducteur (courants de Foucault) . Le système est invariant par rotation autour de l'aze Oz et par translation le long de l'axe ( exception faite des bords). Le champ magnétique crée dans un solénoïde est colinéaire à l'axe Oz du solénoïde et ce champ est invariant par rotation autour de l'axe Oz. B = m0 n i(t) uz. de plus : OM = r ur + z uz. l'expression du potentiel vecteur s'écrit : A = ½m0 n i(t) uz^(r ur + z uz) A = ½m0 n i(t) r uq = ½m0 n r i0 cos (wt)uq pour obtenir l'expression du champ électromoteur -Em, dériver le potentiel vecteur A par rapport au temps : -Em = -½m0 n r i0 w sin (wt)uq Em =
½m0 n r
i0 w
sin (wt)uq
La densité volumique de courant qui prend naissance dans le cylindre est j = g Em. j = ½m0 n r i0 w g sin (wt)uq Le courant circule en boucle dans le
cylindre.
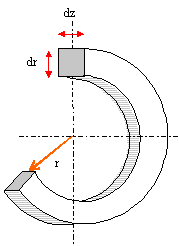
Le tore contient des lignes de courant. L'intensité di qui y circule s'exprime à partir de flux de j à travers la section du tore ds =dr.dz di = j. ds = j uq dr dz uq = j dr dz La résistance élémentaire du tore est : dR = l / ( g ds) = 2pr / ( gdr dz) La puissance élémentaire dissipée à travers le tore est dP = dR (di)² dP = 2pr / ( gdr dz) (j dr dz)² = 2p /g r j² dr dz remplacer j par son expression : dP = 2p /g [½m0 n r i0 w g sin (wt)]² r dr dz dP = ½ p g (m0 n i0 w )² sin² (wt) r3 dr dz puissance moyenne : La valeur moyenne de sin² (wt) est égale à ½. <dP> = 1/4 p g (m0 n i0 w )² r3 dr dz pour l'ensemble du conducteur: intégrer de 0 à R l'expression r3 dr soit 1/4 R4. intégrer dz entre 0 et h soit h. <P> = 1/16 p g (m0 n i0 w )² R4 h. volume du cylindre : V =p R² h <P> = 1/16 g (m0 n i0 w )² R2 V. La puissance moyenne dissipée étant proportionnelle au carré de la pulsation et au volume du cylindre les fours à induction sont d'autant plus efficaces que les pièces sont massives et la fréquence du courant élevée. Par contre dans le cas des transformateurs, il faut limiter les courants de Foucault source d'échauffement et on diminue le volume des pièces métalliques en feuillettant les circuits magnétiques.
|