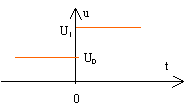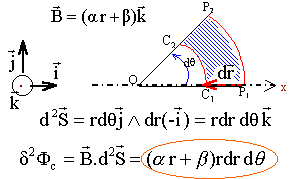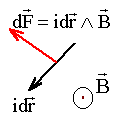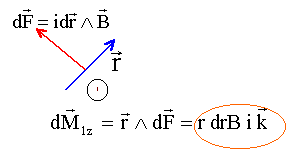Aurélie oct 2001
le phénomène d'induction électromagnétique

Agrég. chimie 91 .

Google

déplacement du circuit dans un champ stationnaire

Dans un laboratoire lié à un référentiel galiléen, un disque solide isolant est en rotation à la vitesse angulaire w autour de son axe Oz. ce solide constitue le rotor d'une machine. On y fixe, en disposition radiale et régulière, N conducteurs rectilignes( tel que AC sur la figure) parcourus par le même courant d'intensité i1. Les conventions de signe correspondant à i1 et w sont indiquées sur la figure.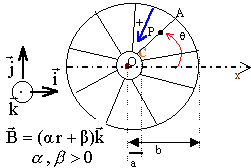

On crée en tout point P tel que OP soit compris entre a et b un champ magnétique indépendant du temps.

  1.  Déterminer la fem induite dans un conducteur par la rotation de ce conducteur dans le champ B, en fonction de w .
  2. Déterminer le moment M1z par rapport à l'axe Oz des forces électromagnétiques subies par ce conducteur en fonction de i1.
  3. Les extrémités des N conducteurs sont reliées entre elles de manière qu'ils soient branchés en parallèle. L'installation absorbe un courant total i =Ni1. Déterminer la fem totale induite dans l'installation ainsi que le moment total Mz, auquel l'ensemble des conducteurs est soumis, en fonction de w et de i.
  4. L'induit d'un moteur électrique à courant continu a un comportement électromécanique analogue à celui des N conducteurs précédents. Electriquement il est alimenté par une source de tension ( fem notée u et résistance R). Les fils qui le constituent, possèdent une résistance r. La fem induite qui apparaît est e = -kew.(ke positive et constant) Il est parcouru par un courant d'intensité i.
    Mécaniquement c'est un solide(S) en rotation autour de l'axe Oz. l'ensemble du moteur et des éléments qu'il entraîne dans son mouvement possède un moment d'inertie J par rapport à Oz. Le moment par rapport à l'axe Oz des forces électromagnétiques est Mz=kmi (km constante positive).
    - Faire un schéma électrique équivalent au circuit de l'induit.
    - Montrez que Mz s'exprime sous la forme : Mz = Au-Bw.
    - Exprimer A et B en fonction de ke, km, R et r.
  5. En réalité la rotation de l'induit s'accompagne d'un frottement visqueux qui se traduit par des forces de moment
    M'z =-lw.( l constante positive). L'induit est alors alimenté par une fem définie par :

    Pout t<0 on admet que le moteur tournait en régime permanent sous l'action de U0. On le soumet à partir de t=0 à un échelon de tension. Déterminer la fonction w (t) et tracer la courbe correspondante.
    ke=0,1 V rad /s ; km= 0,1 N m /A ; R = 20 ohms ; r= 5 ohms et U0=10 V.
    la rotation uniforme sous l'action de U0 s'effectuait à w 0 = 5 tours /s. La constante de temps du régime transitoire qui s'établit est t = 0,1 s. En déduire J et l.

corrigé
Flux élémentaire coupé par une portion élémentaire du segment CA qui passe de P1C1 à P2C2 lors d'une rotation dq pendant l'intervalle de temps dt :

première intégration r variant entre a et b

primitive de (a r2+ b r) : a r3 /3 + b r2 / 2

dFc = [a/3(b3-a3) +b /2 (b²-a²)]dq.

fem induite e = -dFc /dt avec w = dq/dt

d'où : e = -w[a/3(b3-a3) +b /2 (b²-a²)]= -kw .

les fils étant tous montés en dérivation la fem totale est égale à kw.

le circuit élémentaire idl placé dans un champ magnétique est soumis à une force de Laplace telle que :

moment de cette force par rapport à Oz :

remplacer B par son expression B=a r+ b

puis intégrer , r variant entre a et b :

primitive de (a r2+ b r) : a r3 /3 + b r2 / 2

M1z = [a/3(b3-a3) +b /2 (b²-a²)]i = ki

le courant total est Ni1, le moment total est donc Mz = kNi1 = ki.

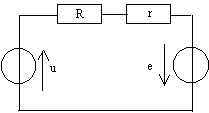
schéma équivalent du circuit :

L'intensité du courant est donnée par la loi de Pouillet : i = (u+e) / (R+r)

Le moment Mz est égal à km i

Mz = km u/ (R+r) + km e/ (R+r) avec e = -ke w.

Mz = km u/ (R+r) - kmke w /(R+r) = Au -Bw.

A = km/(R+r) et B= kmke /(R+r).

appliquer le théorème du moment cinétique au rotor :

dsz/ dt = Mz d'où J dw/dt = Au -Bw.

J dw/dt +Bw= Au.(1)

solution générale de l'équation différentielle du 1er ordre sans second membre :

w(t) = C exp (-t/ t) avec t = J/B.

solution particulière de (1) : w = A/B u.

solution générale de(1) : w(t) = C exp (-t/ t) + A/B u.

à l'instant initial t=0, w est nulle d'où la valeur de la constante C

0 = C+A/B u donne C= -A/B u.

w(t) = A/B u(1-exp (-t/ t).

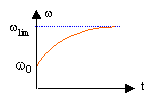
en présence des frottements visqueux, l'équation différentielle devient:

J dw/dt = Au -Bw-lw.

J dw/dt +(B+l)w= Au.(2)

on pose t1 = J / (B+l)

Les conditions initiales sont différentes du cas précédent : à t<0 , w=w0 = A U0 / (B+l)

au bout d'un temps suffisamment long la vitesse limite est : w lim = A U1 / (B+l)

cette vitesse limite représente une solution particulière de (2)

solution générale de l'équation différentielle du 1er ordre sans second membre :

w(t) = D exp (-t/ t1 )

solution générale de(2) : w(t) = D exp (-t/ t1 ) + A U1 / (B+l)

à l'instant initial t=0, w = w0 d'où la valeur de la constante D

w0 = D + A U1 / (B+l)= A U0 / (B+l)

D = A U0 / (B+l) - A U1 / (B+l)

w(t) = A U1 / (B+l)(1- exp (-t/ t1 ) ) + A U0 / (B+l)exp (-t/ t1 ).

applications numériques :

A= 0,1 / (20+5) =4 10-3 N m /V ; B = 0,1*0,1 / 25 = 4 10-4 N m s

w0 =A U0 / (B+l) d'où l= AU0 / w0 -B = 4 10-3*10 / (10*3,14) - 410-4 = 8,73 10-4 N m s.

t1 = J / (B+l) donne J = t1(B+l) = 1,27 10-4 kg m²

retour - menu