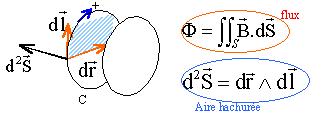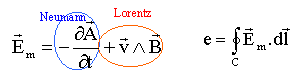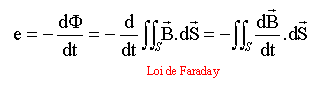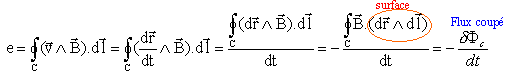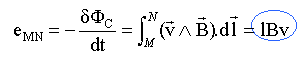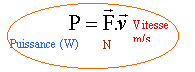|
Agrég. chimie 91 exercice suivant (variation temporelle du champ électromagnétique )
|
||
|
||
|
perméabilité du vide m0 = 4p 10-7 SI
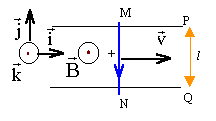
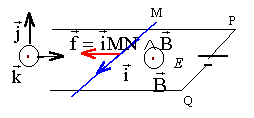
Manifestations de la fem d'induction : On considère le circuit suivant : 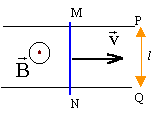 Deux conducteurs parallèles fixes distants de l sont plongés dans un champ magnétique stationnaire uniforme B, vertical. Les deux rails sont horizontaux. La barre métallique MN, de résistance R, de masse m peut se déplacer sans frottements sur les rails. On lui impose un mouvement de translation uniforme, de vitesse v, parallèle aux rails.
corrigé |
||
|
Soit une surface s'appuyant sur le contour C. Le flux du champ magnétique est conservatif et ne dépend pas du choix de la surface; ce flux dépend du contour C.
un petit élément noté dl d'un circuit se déplaçant de dr, balaie la surface hachurée ci dessous. Le flux coupé par l'élément de circuit au cours du déplacement s'exprime par :
Le champ électromoteur est composé de deux termes : - le champ électromoteur de Neuman : "il y a apparition d'un courant induit dans un circuit fermé indéformable, immobile plongé dans un champ magnétique variable". - le champ électromoteur de Lorentz :"il y a apparition d'un courant induit dans un circuit fermé déformé ou déplacé plongé dans un champ magnétique constant". La fem induite e associé au champ électromoteur est égale à la circulation du champ électromoteur sur le circuit C.
deux cas à étudier: - Neumann (circuit fixe et champ variable)
- Lorentz ( circuit mobile et champ magnétique constant)
fem induite:
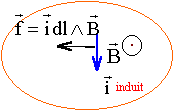
Le sens du corant induit est tel que par ces effets électromagnétiques il s'oppose au déplacement de la barre. La force de Laplace induite est colinéaire à la vitesse mais de sens contraire : d'où le sens du courant induit i ( sens positif choisi)
P et Q en court circuit : écrire la loi d'Ohm i = e /R = Blv / R. entre P et Q un générateur de fem E : écrire la loi de Pouillet i = (e+E) / R= (Blv +E) / R P et Q ouvert : intensité nulle , il apparaît entre les points P et Q la fem induite e force exercée par l'opérateur : le principe d'inertie indique que la barre est pseudo isolée ( somme des forces nulles), le mouvement de MN étant rectiligne uniforme, le référentiel terrestre d'étude étant galiléen. Le poids de la barre est opposé à l'action des rails sur de la barre MN. La barre MN est soumise à la force de Laplace et à la force exercée par l'opérateur : ces deux forces sont opposées. la force exercée par l'opérateur est colinéaire au vecteur vitesse et à le sens de la vitesse. F= Bil. P et Q en court circuit : F= B( Blv/R) l = B²l²v/R entre P et Q un générateur de fem E : F = B((Blv +E) / R)l = B²l²v/R +BEl/R P et Q ouvert : F=0 car l'intensité est nulle. bilan énergétique : P et Q en court circuit :
puissance fournie par l'opérateur : Po= (Blv)² / R puissance dissipée par effet Joule : PJ=Ri² = (Blv)² / R ces deux puissances sont égales : donc l'énergie est conservée entre P et Q un générateur de fem E : puissance fournie par l'opérateur : Po= (Blv)² / R + EBlv/R puissance dissipée par effet Joule : PJ= Ri² = (E+Blv)² / R puissance délivrée par la source :P= Ei = E ( E+Blv)/R Po+ P = PJ; conservation de l'énergie
barre livrée à elle même : appliquer le théorème du centre d'inertie dans le référentiel terrestre supposé galiléen. la barre est soumise à son poids, à l'action des rails opposées au poids tant qu'il y a contact et à la force de Laplace.
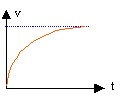
Projection sur l'axe Ox : mdv/dt = - (EBl+B²l²v)/R m dv/dt + B²l²/R v = - EBl/ R la vitesse limite est une solution particulière de cette équation : vlim = E/(Bl). solution générale de l'équation sans second membre : v = A exp (-B²l²/(mR) t) solution générale : v = A exp (-B²l²/(mR) t) +E/(Bl). à t=0, la vitesse est nulle d'où A = -E/ (Bl) v = E/ (Bl) ( 1-exp (-B²l²)/(mR) t)).
retour - menu |