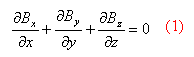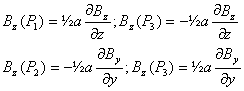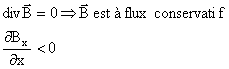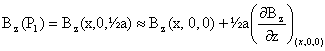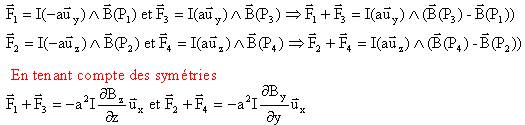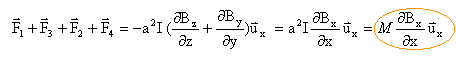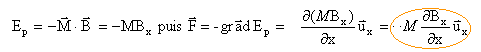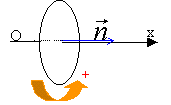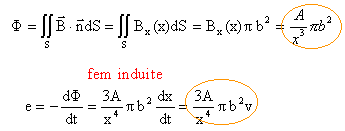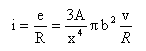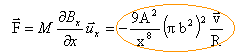|
Capes 97 .
|
||
|
||
|
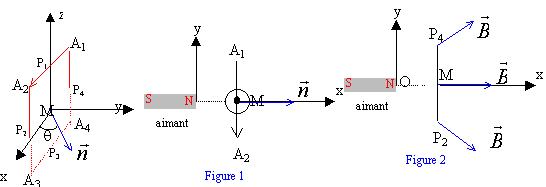
Une petite spire carrée de coté a, mobile autour d'un axe D=Mz , est placée au voisinage d'un aimant droit fixe qui crée un champ magnétique non uniforme (figure 1) . Le coté a est suffisamment faible pour que l'on puisse admettre que : - la force F qui s'exerce sur l'un des cotés peut être évaluée en considérant que le coté est est dans un champ magnétique uniforme . - la spire est soumise à un couple dont le moment par rapport à l'axe D est : MD = -M B sin q avec M le moment magnétique de la spire. - la spire posséde l'énergie potentielle Ep= -MB cosq. Les échelles ne sont pas respectées (figures 1 et 2). Le champ magnétique crée par l'aimant en un point de coordonnées x, y, z a pour composantes Bx, By, Bz. Une représentation dans le plan (O, Ox, Oy) est donnée figure 2. On dispose des informations suivantes : - En M (x, 0, 0): Bx= Bx(x, 0, 0); By = Bz=0 par raison de symétrie - - par raison de symétrie , on écrit : Bx(P1) = Bx(P3) et Bx(P2) = Bx(P4) - en (x, 0, 0)
corrigé |
||
|
le champ décroît quand on s'éloigne de l'aimant.
faire un développement limité au voisinage de z=0
on effec tue la somme de ces quatre forces en teant compte de la relation (1) :
la somme des forces peut être déterminée à partir de l'énergie potentielle:
l'intensité I va de A1 vers A2 (figure 1), le moment magnétique de la spire est dirigé suivant Ox ,soit M>0 dBx / dx est négatif la somme des forces est donc dirigée suivant -Ox: la spire est attirée par l'aimant. si l'on change le sens du courant
dans la spire, le moment magnétique change de sens et
également la force: dans ce cas la spire et l'aimant
se repoussent.
La spire se déplace dans une région où règne un champ magnétique variable: elle est donc parcourue par un courant induit du fait de la variation du flux.. la f.e.m induite est donnée par e = - dF /dt. choix d'un sens de parcours sur la spire:
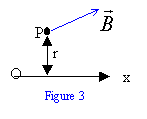
expression du flux du champ magnétique à travers la spire ( Br étant ortoradial à n)
l'intensité du courant induit i sera alors:
moment magnétique de la spire :
vecteur force et vecteur vitesse de sens contraire
on met en évidence le freinage par courant induit ( sur les véhicules lourds) |