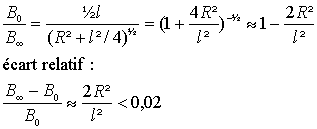|
Capes interne 94 exercice suivant (tore)
|
||
|
||
|
On considère une bobine longue sans noyau de fer , dont les caractéristiques sont les suivantes: N=200 spires; longueur ;l = 40 cm; rayon moyen des spires : R= 2,5 cm.
corrigé |
||
|
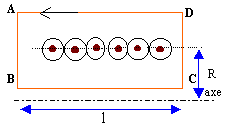
Champ du solénoïde : Tout plan perpendiculaire à l'axe de la bobine est un plan de symétrie pour le courant : en conséquence, le champ magnétique est perpendiculaire à ce plan. La distibution de courant étant invariante par rotation autour de l'axe de la bobine, et par translation sur cet axe, le champ est porté par l'axe de la bobine et ne dépend que de la distance à l'axe. Le champ est nul à l'extérieur de la bobine, car les lignes de champ ne sortent pas du solénoïde. Appliquons le théorème d'Ampère au contour ABCD
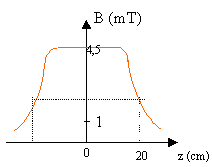
le champ étant perpendiculaire à AB et à CD, la circulation est nulle le long de AB et CD le champ est nul à l'extérieur, la circulation du champ est nulle le long de AD la circulation du champ est m0N I le long de BC m0N I = B l B= m0n I avec n= N/ l , nombre de spire par mètre. le champ est uniforme et colinéaire à l'axe à l'intérieur du solénoïde. A.N : B= 4p 10-7 * 200 / 0,4 * 7 = 4,39 mT. cette valeur est 220 fois plus grande que la valeur de la composante horizontale du champ magnétique terrestre.
B S = LI soit m0N I / l pR² =L I à travers N spires : m0N² I / l pR² =L I L= m0N² / l pR² L=4p 10-7 * 200² / 0,4 *p *0,025² = 0,247 mH.
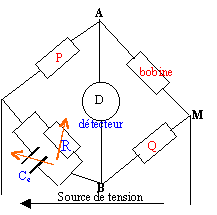
Le filtre réglé sur la fréquence d'étude 400 Hz élimine les parasites L'équilibre du pont est réalisé la tension aux bornes du détecteur est nulle. On règle Re et Ce afin que cette tension soit nulle. (toutes les grandeurs écrites en rouge ci dessous sont des nombres complexes) uAB= uAM+ uMB= 0 à l'équilibre du pont soit uAM= - uMB impédance complexe de la bobine ZB= R+jLw. impédance complexe Ze du condensateur et de Re en dérivation : 1 / Ze = 1/ Re + jCew. uAM = Q / (Q+Ze ) e et uBM= ZB / (P+ZB) e . e est l'amplitude complexe de la source de tension Q / (Q+Ze ) = ZB / (P+ZB) PQ + QZB= QZB + ZBZe PQ =ZBZe exprimons L et R : ZB = PQ(1/ R0 + jC0w)= PQ / R0 +jPQC0w = R+jLw. R= PQ / R0 et L= PQC0 A.N : R=1,25 ohm et L= 0,241 mH. l'écart avec l'inductance, calcul théorique, n'excède pas 3%; cette méthode de mesure est correcte.
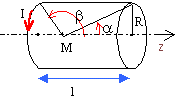
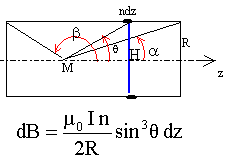
On pose MH= z; z = R cotanq et dz = -Rdq / sin²q et dB= - ½m0 I n sinq dq intégrer entre les valeurs b et a. B= ½m0 I n (cos a- cosb) pour un solide infiniment long a tend vers 0 et b tend vers p: on retrouve Boo=m0 I n au centre du solénoïde : p = a+b. Bo = m0 I n cos a. avec cos a : ½ l / (R²+l²/4)½. Boo = m0 I n
si la longueur est supérieure à 10 fois le rayon le solénoïde peut être considéré comme infini.
retour - menu |