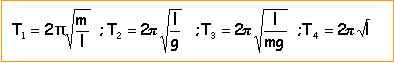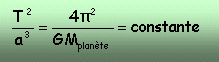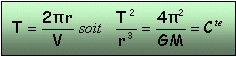| |
|
||||||
| |
|
||||||
|
|
Les pendules de Galilée |
corrigé |
|||||
| |
allée et venue; vibration. position perpendiculaire Entre la période du corps pesant et celle du corps léger, la coïncidence est telle que... Pour une longueur donnée de quatre coudées chacun, la période est indépendante de la masse. Le texte ne donne aucune information concernant l'influence de la longueur du fil. On pourra proposer de faire l'expérience avec deux fils de longueur différente avec des boules identiques ou non puisque la masse n'intervient pas.
T indépendant de m donc on peut éliminer T1 et T3 . T2 seul est homogène à un temps. rac carrée de [ longueur (m) / ms-2] T = 2,8 s Les deux pendules ont " un rythme de mouvement rigoureusement identique " donc à chaque instant ils ont la même vitesse. N'ayant pas la même masse, lors du passage par leur position d'équilibre ils ont des énergies cinétiques différentes. énergie mécanique constante pour chaque pendule. ou bien : les deux pendules ont une énergie potentielle initiale différente : même h mais m différent . Leur vitesse initiale étant nulle leur énergie cinétique maximale est égale à leur énergie potentielle initiale donc différente. (conservation de l'énergie mécanique de chaque pendule).
|
||||||
|
lois de Kepler (origine : ac-Lille) |
corrigé |
||||||
| |
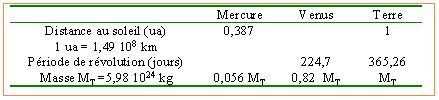
première loi de Newton (principe de l'inertie) Dans un référentiel galiléen, lorsqu'un solide est isolé ou pseudo-isolé (somme des forces égale vecteur nulle), son centre d'inertie G est : soit au repos si G est initialement immobile soit animé d'un mouvement rectiligne uniforme ( le vecteur vitesse est un vecteur constant) Dans le cas de la terre tournant autour du soleil : carré de la période (seconde) =(365,26*24*3600)² = 9,94 1011 s² rayon au cube de l'orbite (distance en mètre) (1,49 1011)3 = 3,3 1033 m3. T² / a3 = 3 10-19 . d'où la masse du soleil (kg): 3 10-19 = 4*3,14² /(6,67 10-11 *Msoleil) Msoleil =39,44 /(6,67 10-11 * 3 10-19 )= 1,97 1030 kg. période de révolution de mercure : T²= 3 10-19 *(0,387*1,49 1011)3 = 5,75 1013 s² T= 7,584 106s = 87,7 jours. distance soleil à vénus : a3 = (224,7*24*3600)² / 3 10-19 = 1,25 1033 m3. a = 1,08 1011 m = 0,724 ua. distance terre à la lune : nouvelle valeur de la constante, laterre étant l'astre central 4*3,14² / (6,67 10-11*5,98 1024) = 9,88 10-14. a3 =(27,32*24*3600)² /9,88 10-14 = 5,64 1025. a = 3,83 108 m.
|
||||||
 3 3
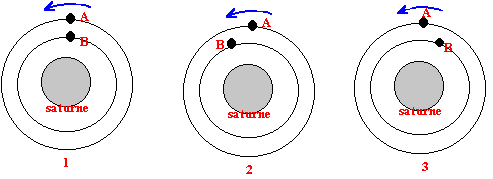
les anneaux de saturne
|
"On pourrait croire que les anneaux de Saturne sont d'un seul tenant. En fait, il s'agit de nuées de pierrailles, dispersées tout au long du plan équatorial, qui circulent en orbites individuel-les autour de la planète." Hubert Reeves (Poussières d'étoiles) Le but de cet exercice est de juger la compatibilité d'un modèle avec la deuxième phrase de cette citation.
corrigé |
||||||
| |
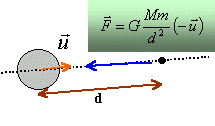
L'interaction de gravitation où G désigne la constante de gravitation, r la distance entre le centre O de la planète et l'objet et u, un vecteur unitaire centré en O et dirigé vers l'objet.
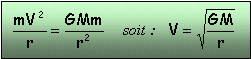
Satellite sur une orbite circulaire Le référentiel utilisé est un référentiel, analogue au référentiel géocentrique, ayant pour origine le centre de la planète et dirigé vers des étoiles "fixes" ; on le suppose galiléen. La force est centrale et normale à la trajectoire ; l'accélération tangentielle est donc nulle. Ceci implique que la norme de la vitesse reste constante. Le principe fondamental, appliqué à l'objet de masse m indique que :
Le mouvement est uniforme donc :
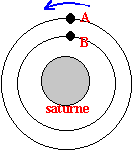
Objets sur une même orbite On a vu que la masse de l'objet satellite n'intervenait pas dans les expressions de V et de T. Sur une même orbite circulaire, tous les objets ont la même vitesse et la même période. La structure de l'ensemble des objets, distance et rayon de l'orbite ne se modifie donc pas au cours du temps. Objets sur des orbites de rayons différents La loi de Kepler indique que T augmente si r augmente ; l'objet A a donc une période TA plus grande que TB, celle de l'objet B. Ce dernier parcourt donc son orbite plus rapidement et met moins de temps pour faire un tour ; il passe donc en "avance" par rapport à A. C'est donc la configuration 2 qui est possible. Les anneaux de Saturne Les différentes particules qui constituent un anneau sont sur des orbites de rayons pratiquement identiques ; elles ont donc toutes la même période. L'anneau, tout entier, tourne autour de Saturne avec une vitesse angulaire qui dépend de son rayon. Les différents anneaux tournent autour de Saturne avec des vitesses angulaires plus grandes pour les anneaux proches que pour les anneaux lointains ; ils "glissent" les uns par rapport aux autres. Si un anneau était très large, les différences de vitesse entre la périphérie de l'anneau et la partie intérieure provoqueraient des tensions et, à la longue, ces différentes parties finiraient par se disloquer.
|
||||||
| |
|
||||||
|
|
|