|
1- Décroissance radioactive
:
Un échantillon de matière radioactive est placé dans la
chambre d 'un photomultiplicateur. Un détecteur, associé au
photomultiplicateur, mesure un nombre d'événements, pendant une durée Dt déterminée. On trace la courbe d'évolution du
nombre d'événements mesuré par seconde (noté x), au cours du temps.
Soit x0 la valeur de x à l'instant choisi pour origine des
dates. On réalise des mesures avec des échantillons de radon22086Rn
et de radon 22286Rn qui sont des émetteurs a.
Le tableau ci-dessous résume les conditions expérimentales de
cette étude:
|
expérience1
|
expérience 2
|
expérience3
|
|
Grandeurs caractéristiques du système :nature du
noyau
|
radon 220
|
radon 220
|
radon 222
|
|
Conditions initiales : population initialede noyaux
radioactifs N0 différent N0' différent N0''
|
N0
|
N0'
|
N0''
|
|
Paramètres extérieurs
|
Aucune modification des paramètres extérieurs
|
|
Temps caractéristique
|
t½ =55,5 s
|
t½ =55,5 s
|
t½ = ??
|
Les courbes correspondant à cette étude et donnant l'évolution
de x au cours du temps sont représentées :
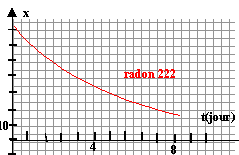
- Définir le temps de demi-vie (ou demi-vie).
- La loi de décroissance radioactive s'écrit sous la forme N
= N0 e-lt
où :
N est le nombre de noyaux radioactifs présents à l'instant de date t, N0
est le nombre de noyaux radioactifs présents à l'instant choisi pour
origine des dates t0 = 0 s, l
est la constante radioactive. En utilisant la définition du temps de
demi-vie, établir l'expression de l en
fonction de t½.
- Dans le cas de l'expérience 3, déterminer graphiquement la
valeur du temps de demi-vie. Pour cette détermination, on admettra que
le nombre d'événements détectés par seconde, à l'instant de date t, est
proportionnel au nombre de noyaux radioactifs présents dans
l'échantillon, à cette méme date. Pour déterminer le temps de demi-vie,
on peut alors utiliser la courbe x = f (t) de la même façon que celle
représentant le nombre de noyaux radioactifs présents dans
l'échantillon en fonction du temps.
- En justifiant les réponses à partir des données du tableau
et du résultat obtenu à la question 1.3. préciser :
- Si les grandeurs caractéristiques ont une influence sur la valeur du
temps de demi-vie ;
- Si les conditions initiales ont une influence sur la valeur du temps
de demi-vie.
II. Charge d'un condensateur à
travers un conducteur ohmique :
Soit un dipôle RC constitué d'un condensateur de capacité C
réglable et d'un conducteur ohmique de résistance R réglable. On étudie
la charge du condensateur à travers le conducteur ohmique. Pour cela,
on réalise le montage de la figure ci-dessous.
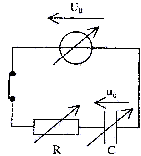
Le générateur délivre, à ses bornes, une tension constante U0
réglable. Au cours d'une expérience avec acquisition et traitement
informatisés des données, on enregistre les variations de la tension uC
aux bornes du condensateur au cours du temps. A chaque nouvelle
expérience, on ne change qu'une seule des conditions expérimentales. Le
tableau ci-dessous résume les conditions expérimentales de cette étude :
|
expérience 1
|
expérience 2
|
expérience 3
|
expérience 4
|
|
Grandeurs caractéristiques du système
|
R = 20 kW
|
R = 20 kW
|
R = 10 kW
|
R = 20 kW
|
|
C = 31 µF
|
C = 31 µF
|
C = 31 µF
|
C = 12,5 µF
|
|
Conditions initiales : uC(à t0 = 0 s) =
0,0 V
|
Aucune modification des conditions initiales
|
|
Paramètres extérieurs
|
U0 = 4,25 V
|
U0 = 5 V
|
U0 = 4,25 V
|
U0 = 4,25 V
|
|
Temps caractéristique
|
t1 = 0,62 s
|
t2 = 0,62 s
|
t3 = 0,31 s
|
t4 = ??
|
Les courbes correspondant à cette étude et donnant l'évolution de la
tension uC au cours du temps sont représentées :
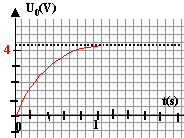
- Dans le cas de l'expérience 4, déterminer graphiquement par
une méthode au choix, la constante de temps du circuit. La méthode sera
explicitée et la détermination devra apparaître clairement sur la
courbe.
- En justifiant les réponses à partir des données du tableau
et du résultat obtenu à la question 2.1., préciser :
- Si les grandeurs caractéristiques ont une influence sur la valeur de
la constante de temps ;
- Si les paramètres extérieurs ont une influence sur la valeur de la
constante de temps.
- Plusieurs expressions de la constante de temps t d'un circuit RC sont proposées ci-dessous
:
t = U0 RC (1) ; t = U0 / (RC) (2) ; t = R/C ; t = C /
R (4) ; t = RC (5) ; t
= racine carrée (RC) (6)
- À partir de l'étude expérimentale précédente, justifier
qu'une seule expression est à retenir.
- Vérifier par une analyse dimensionnelle l'expression de la constante
de temps trouvée à la question précédente.
III. Chute avec frottements
:
À partir d'une même position de l'espace, on réalise dans deux
fluides différents, la chute verticale sans vitesse initiale de solides
de petites dimensions, de même forme, de même volume, mais de masses
différentes. On filme la chute et un dispositif informatique permet de
tracer la courbe donnant l'évolution de la vitesse v du centre
d'inertie du solide en fonction du temps.
À chaque nouvelle expérience, on ne change qu'une seule des
conditions expérimentales. Le tableau ci-dessous résume les conditions
expérimentales de cette étude :
|
expérience 1 : solide A
|
expérience 2 : solide A
|
expérience 3 : solide B
|
|
Grandeurscaractéristiques du système
|
volume V
|
volume V
|
volume V
|
|
masse m
|
masse m
|
masse m' différente de m
|
|
Conditions initiales :Position initiale,Vitesse
initiale
|
Aucune modification des conditions initiales
|
|
Paramètres extérieurs
|
fluide : eau
|
fluide : détergent
|
fluide : eau
|
|
Temps caractéristique
|
t1 = 0,21 s
|
t2 = 0,15 s
|
t3 = ??
|
Les courbes correspondant à cette étude et donnant l'évolution de la
vitesse v au cours du temps sont représentées :
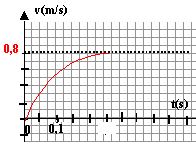
- Dans le cas de l'expérience 3, déterminer graphiquement le
temps caractéristique.
- En justifiant les réponses à partir des données du tableau
et du résultat obtenu à la question 3.1.,préciser :
- Si les grandeurs caractéristiques ont une influence sur la valeur du
temps caractéristique ;
- Si les paramètres extérieurs ont une influence sur la valeur du temps
caractéristique.
- Lors de la chute verticale d'un solide dans un fluide, le
mouvement comporte deux phases :
- une première phase correspondant au " régime initial " ,
- une seconde phase correspondant au " régime asymptotique".
En justifiant la réponse, préciser sans calcul la nature du mouvement
du centre d'inertie du solide en chute :
- au cours du régime initial;
- au cours du régime asymptotique.
IV. Bilan :
Sans étude complémentaire, compte-tenu des expériences
réalisées et des réponses aux questions 1.4., 2.2 et 3.2., analyser
pour l'ensemble des trois systèmes étudiés, chacune des propositions
données ci-dessous :
- le temps caractéristique dépend des grandeurs caractéristiques du
système (proposition 1);
- le temps caractéristique dépend des conditions initiales (proposition
2);
- le temps caractéristique dépend des paramètres extérieurs
(proposition 3).
Si la proposition est vérifiée simultanément pour les trois
systèmes étudiés, on indiquera : proposition juste.
Si la proposition n'est pas vérifiée simultanément pour les
trois systèmes étudiés, on indiquera: proposition fausse.
Si les informations données sont insuffisantes pour conclure,
on indiquera: informations insuffisantes
Aucune justification n'est demandée.
corrigé
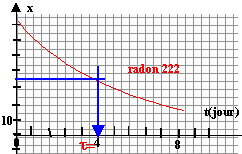
demi-vie ou période : durée au bout de laquelle la
moitié des noyaux initiaux se sont désintégrés
d'après le graphe t½ = 4 jours.
½N0 = N0 exp (-lt½)
½ = exp (-lt½) ; ln½ = - lt½ ; - ln 2 = - lt½
; ln2 = lt½ ;
t½ dépend de la nature du noyau radioactif.
t½ ne dépend pas du nombre initial de noyaux.
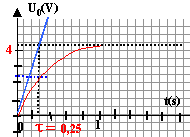
tracer la tangente à l'origine : elle coupe l'asymptote à t = t = 0,25 s
ou bien à t =t, la tension aux
bornes du condensateur vaut 0,63 U0 : tracer une hotizontale
passant par u = 0,63 U0 ; à partir de l'intersection avec la
courbe tracer une verticale .
R et C ont une unfluence sur t.
la tension U0 n'a pas d'influence sur t.
si R est divisée par 2, alors t
est divisée par 2
si C est multipliée par 0,4 alors t
est multipliée par 0,4
t est proportionel à R et à C ce
qui ne laisse que les expressions (1) et (5).
R, résistance en ohm soit tension(volt) / intensité (ampère) :
[V][A]-1.
C capacité en farad soit charge (coulomb) / tension (volt)
charge (coulomb) = intensité (ampère) fois temps (seconde)
d'où C : [A][s][V]-1.
en conséquence RC s'exprime en seconde. ( expression (5)
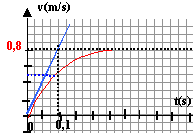
la masse a une influence sur t.
la nature du fluide a une influence sur t.
au tout début de la chute, chute libre
le régime asymptotique correspond à un mouvement rectiligne
uniforme.
(1) est vraie.
(2) informations insuffisantes ( ce n'est pas vérifié pour le
dipôle RC et les conditions initiales sont inchangées pour la chute)
(3) informations insuffisantes ( les paramètres extérieurs
sont inchangées pour le radon)
|






