Aurélie 09/03

oscillations libres et forcées Réunion 03

sans calculatrice


Google



Pour modéliser le ressort d'une suspension de voiture on utilise un ressort de raideur k=40 N/m.
I- étude statique : il s'agit de déterminer la constante de raideur k. On mesure la longueur du ressort seul ( à vide) L0 = 10 cm ; on suspend une masse m=100 g et on mesure une longueur L= 12,4 cm ; g = 10 m/s² ; 1/2,4 = 0,42 ; 1/ 3,2 = p/10.

  1. Calculer la valeur k1 de la raideur.
  2. Quelle est l'erreur relative par rapport à la valeur k donnée ?

II- étude dynamique : on utilise un système approprié d'acquisition permettant d'obtenir la courbe ci-dessous : ( oscillations sans frottement)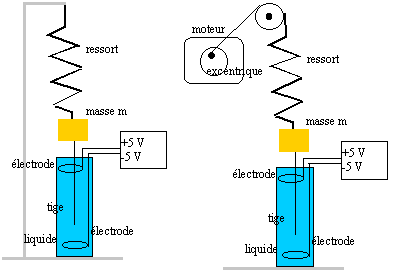

  1. Déterminer la période de l'oscillateur.
  2. Cette valeur est-elle en accord avec la valeur théorique T= 2p [m/k]½.
  3. Sachant que le newton a la dimension kg m s-2 montrer que T s'exprime en seconde.
  4. Dans le dispositif on remplace la solution conductrice précédente par une autre solution plus visqueuse. Dessiner la courbe obtenue.

III- Oscillations forcées : l'extrémité du ressort est fixée à un excentrique entraîné par un moteur. On réalise plusieurs enregistrements pour différentes vitesse de rotation (ou fréquence en Hz) du moteur. On relève l'amplitude de chaque courbe :
f(Hz)
1,5
2
2,5
2,8
3,1
3,2
3,3
3,6
4
4,5
xmax(cm)
0,4
0,6
1
1,5
2,1
2,3
2
1,5
1
0,7

  1. Quel est le rôle du moteur et de l'excentrique ?
  2. Quel est le nom du système {ressort vertical + masse} ?
  3. Quel phénomène obtient-on pour f = 3,2 Hz ? En déduire la période des oscillations à la résonance et la comparer à celle des oscillations libres.
  4. Quelle observation ferait-on dans le cas où la viscosité de la solution augmenterait ?

IV- Suspension d'une automobile : Le système de suspension comprend des ressorts et des amortisseurs. La voiture constitue un système oscillant à la fréquence propre f0. Certaines pistes ont l'aspect de tôles ondulées ( successions de trous et de bosses à intervalles réguliers L). Pour une vitesse VR, la voiture subit des oscillations de forte amplitude.

  1. Expliquer ce phénomène en précisant le rôle de la piste.
  2. Exprimer la vitesse VR en fonction de f0 et L.
  3. Calculer cette vitesse ( en km/h) si f0 = 5 Hz et L=80 cm.

 

corrigé
à l'équilibre statique, le poids et la tension du ressort sont opposées : ces deux forces ont la même norme.

mg = k1(L-L0) soit k1 = mg / (L-L0) = 0,1*10 / ((12,4-10) 10-2)=100/2,4 = 42 N/m.

erreur relative : (42-40) / 40 = 0,05 (5%)

période T0 = 0,33 s ( lecture graphe)

par le calcul : T0 = 2*3,14 [0,1/40]½=6,28 * 0,05 = 0,314s. donc accord

2p sans dimension ; masse en kg ;

raideur en newton mètre-1; soit kg m s-2 m-1 soit kg m s-2

masse / raideur : kg kg-1 s2 soit s2

(m/k)½ en seconde

si la solution est plus visqueuse, les frottements sont plus importants : amortissement

moteur + excentrique = excitateur

ressort + masse = résonateur

à f = 3,2 Hz, résonance : l'amplitude du résonateur devient maximale.

à la résonance la période de l'excitateur est égale à la période propre du résonateur : 1/3,2 = 0,314 s.

Avec une solution plus visqueuse ( frottement) la résonance sera moins aigue ( résonance floue) et peut même disparaître si l'amortissement est grand.

piste déformée = excitateur

suspension = résonateur

 si la fréquence imposée par la piste devient égale à la fréquence propre de la suspension ( et si l'amortissement est faible) on observe un phénomène de résonance.

vitesse (m/s) = distance des creux (m) * fréquence (Hz)

v= Lf0 = 0,8*5 = 4 m/s = 4*3,6 km/h = 14,4 km/h.

à suivre
retour - menu
à bientôt ...