|
avec calculatrice |
||||||
|
||||||
|
|
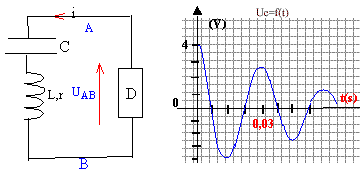
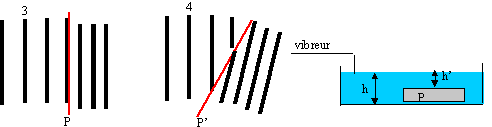
Pour étudier les ondes progressives à la surface de l'eau on utilise une cuve à ondes. Un vibreur permet de générer des ondes planes circulaires de fréquence N à la surface de l'eau. Les crêtes des vages donnent des rides brillantes et les creux ds rides sombres sur un écran. AB= 7 cm. A- étude du vibreur : La surface de l'eau est excitée par de l'air pulsé: les pulsations sont crées par une petite pompe. Leur fréquence peut être régle de 10 à 40 Hz gràce à un oscillateur électrique entretenu. Les oscillations électriques peuvent être obtenues gràce à un condensateur de capacité C= 30mF relié à une bobine d'inductance L et de résistance r.
B- Etude des ondes.
oscillations libres amorties. E0 = ½CU2c(t=0) =0,5 * 30 10-6 *42 =2,4 10-4 J. E1 = ½CU2c(t=30 ms) =0,5 * 30 10-6 *2,52 =9,4 10-5 J. dissipation d'énergie dans la résistance r lors des échanges d'énergie entre condensateur et bobine. Ce dispositif
amorti ne peut être utilisé.
oscillations sinusoïdales périodiques : le montage peut alors être utilisé. N= 1 / (2p (LC)½)= 1 / [6,28 (0,75*30 10-6)½]
= 33,5 Hz.
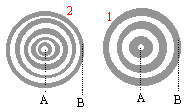
AB= 7 cm ; deux crètes sont distantes de l ; deux creux sont distants del. photo 1 : AB=0,07 = 2,5 l 1 d'où l 1 = 0,028 m. v1 =l 1 N1 =0,028*8 = 0,224 m/s. photo 2 : AB=0,07 = 4,5 l2 d'où l 2 = 0,0155 m. v2 =l 2 N2 =0,0155*17 = 0,26 m/s. La surface de l'eau est un milieu dispersif pour les ondes mécaniques. le verre est un
milieu dispersif pour la lumière : la lumière blanche est dispersée et
on observe, émergeant du prisme, toutes les couleurs de l'arc en ciel (
le bleu est le plus dévié)
à droite, la distance entre deux crètes successives est l 2 . l 1 est différent de l 2 ; N est constante et v = l N donc la célérité v dépend de la profondeur h. photo 4 : phénomène de diffraction : changement de la direction de propagation de l'onde. v1 = 9,8 / 6,28* (1/5) = 0,312 m/s l1 = v 1 /N1 =0,312 / 5 =0,062 m v2 = 9,8 / 6,28* (1/10) = 0,156 m/s l2 = v 2 /N2 =0,156 / 10 = 0,0156 m M reproduit le mouvement de la source avec un retard t1 = MS / v1 = 10 / 0,312 = 32 s de même t2 = MS/v2 = 10 / 0,156 = 64 s.
|
|||||
|