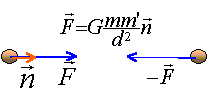texte : le premier lanceur Ariane est une fusée ) trois étages dont la hauteur totale est de 47,4 m et qui pèse, avec sa charge utile (satellite), 208 tonnes au décollage. Le premier étage, qui fonctionne pendand 145 s est équipé de 4 moteurs Viking V alimentés par du peroxyde d'azote N₂O₄ ( masse de peroxyde emportée 147 tonnes). L'intensité de la force de poussée totale F de ces 4 moteurs est constante pendant leur fonctionnement : elle vaut F= 2445 kN.

Le lanceur peut mettre en orbite circulaire basse de 200 km d'altitude un satellite de 4850 kg. Il peut également placer en orbite géostationnaire un satellite de 965 kg. Il peut être aussi utilisé pour placer en orbite héliosynchrone des satellites très utiles pour les applications météorologiques.

1. L'ascension de la fusée Ariane :
   Le champ de pesanteur est supposé uniforme : g₀ = 9,8 m/s². On choisit un axe Oz vertical vers le haut. On étudie le mouvement de la fusée dans le référentiel terrestre supposé galiléen
   a- Représenter sur un schéma en les nommant les deux forces qui agissent sur la fusée Ariane lorsqu'elle s'élève verticalement. On néglige les frottements et la poussée d'Archimède
   b- A un instant quelconque, la masse de la fusée est m. Déterminer en fonction de m et des intensités des deux forces précédentes la valeur de l'accélération a.
   c- On considère d'abord la situation au décollage. La masse de la fusée vaut alors m₁. Calculer la valeur numérique de l'accélération a à cet instant. On envisage la situation qui est celle immédiatement avant que tout le peroxyde d'azote ne soit consommé. La masse de la fusée vaut alors m₂ . Calculer la valeur numérique de m₂ puis celle de l'accélération a₂ à cet instant. Le mouvement de la fusée est-il uniformément accéléré ?
   d- La vitesse d'éjection V_e des gaz issus de la combustion du peroxyde d'azote est donnée par la relation : ( les vecteurs sont écrits en bleu et en gras) V_e = Dt / D m F. où Dt / D m est la variation de la masse de la fusée par unité de temps et caractérise la consommation des moteurs. Vérifier l'unité de V_e par analyse dimensionnelle. Calculer la valeur numérique de V_e. Quel est le signe de Dt / D m ? En déduire le sens de V_e. Qu'en pensez vous ?
   A l'aide d'une loi connue que l'on énoncera, expliquer pourquoi l'éjection des gaz propulse la fusée vers le haut.
2. Etude du satellite situé à basse altitude h=200 km : on s'interesse au mouvement d'un satellite S, de masse m_S, en orbite circulaire ( rayon r) autour de la terre de masse M_T, de rayon R_T et de centre O.On suppose que la terre est une sphère et qu'elle présente une répartition de masse à symétrie sphérique et que le satellite est assimilé à un point.
   a- Préciser les caractéristiques du vecteur accélération a d'un point animé d'un mouvement circulaire uniforme de rayon r et de vitesse v.
   b- Enoncer la loi de gravitation universelle. On appelle G la constante de gravitation universelle. Faire un schéma sur lequel les vecteurs forces sont représentés.
   c- Le satellite est à l'altitude h tel que r=R_T+h. On appelle F_S la force qu'exerce la terre sur le satellite. Cette force dépend de la position du satellite et on pose F_S = m_S g(h). On note g(h) l'intensité de la pesanteur à l'endroit où se trouve le satellite. Exprimer g(h) en fonction de M_T, R_T, G et h puis en fonction de R_T, h et g₀.
   d- Appliquer la deuxième loi de Newton au satellite en orbite circulaire. En déduire l'expression de la vitesse v_S du satellite en fonction de g₀, R_T et h puis celle de sa période T_S.
   e- Application numérique : g₀ = 9,8 m/s² ; h=200 km et R_T= 6400 km. Calculer v_S et T_S.

---

---

corrigé

---

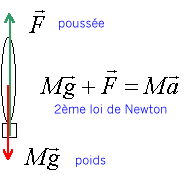
sur un axe Oz vertical vers le haut : F-Mg=Ma

a = F/M -g₀.

a₁ = 2,445 10⁶ / 2,08 10⁵ -9,81 = 1,94 m/s².

m₂ = 208-147,5 = 60,5 t = 6,05 10⁴ kg

a₂ = 2,445 10⁶ / 6,05 10⁴ -9,81 = 30,6 m/s².

l'accélération n'est pas constante : le mouvement n'est pas uniformément accéléré.

---

V_e = Dt / D m F.

force = masse * accélération ; force : [kg] [L][T]^-2 ;

Dt / D m F : [T] [kg] ^-1 [kg] [L][T]^-2 = [L][T]^-1 ( mètre / seconde)

consommation des moteurs : 1,475 10⁵ / 145 = 1017,5 kg/s

Dt / D m = 1/1017,5 = 9,38 10^-4s/kg.

Ve = 9,38 10^-4* 2,445 10⁶ = 2403 m/s.

D m est négatif, car la masse de la fusée diminue ; Dt positif ;

V_e et F colinéaires mais de sens contraire ; F est dirigée vers le haut ; V_e est dirigée vers le bas.

principe des actions mutuelles ( 3 ^ème loi de Newton) ou principe de l'action et de la réaction :

Si un corps A (fusée) exerce sur un corps B ( gaz éjectés) une force F_A-->B , inversement B exerce sur A une action opposée F_B-->A = - F_A-->B

---

loi de gravitation :

Soit deux corps A et B de masse m et m' distant de d :

entre les deux corps s'exercent des forces attractives proportionnelles aux masse (kg) et inversement proportionnelles au carré de la distance (m) qui les séparent. La constante de proportionnalité est G, constante de gravitation universelle.

---

l'accélération est centripète, dirigée vers le centre du cercle

---

g₀ = GM_T / R_T² soit GM_T= g₀ R_T²

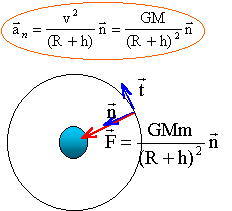
g(h) = GM_T /(R_T+h)² = g₀ R_T²/(R_T+h)²

la relation fondamentale de la dynamique ( 2ème loi de Newton) projetée sur l'axe n de la base de Frenet donne :

V² / r = G M_T / r² = g₀ R_T² / (R_T+h)

d'où V² = G M_T / r avec r = (6400+200) 10³ = 6,6 10⁶ mètres

V² = 9,81 * (6,6 10⁶ )² / 6,6 10⁶ = 6,09 10⁷.

V=7800 m/s.

la période T est la durée nécessaire pour parcourir une circonférence à la vitesse V

2pr = V T

4p²r² = V² T²

remplacer V² par l'expression ci dessus.

4p²r² =g₀ R_T² / r T² ;

soit T² = 4 p ² r³ / (g₀ R_T²) ( 3ème loi de Kepler)

T = 2pr / V = 6,28 *6,6 10⁶ / 7800 = 5,3 10⁶ s.

---