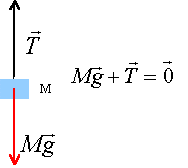On détermine par trois méthodes différentes la raideur dun resort

A étude statique :

Le ressort étudié est accroché à une potence. A l'extrémité libre E on suspend successivement des masses de différentes valeurs. Pour chaque masse m on mesure l'allogement Dl du ressort.

masse m (kg)	0	0,2	0,4	0,5	0,7	1
Dl (m)	0	0,05	0,1	0,125	0,175	0,249

1. En déduire la relation numérique entre m et Dl .
2. Donner les caractéristiques des forces qui agissent sur la masse m. Exprimer leur somme à l'équilibre; justifier.
3. En déduire l'expression litérale de la constante de raideur k. Donner l'unité de cette constante. Vérifier l'homogénéité de l'expression par analyse dimensionnelle; calculer k.

B étude dynamique :

Le ressort précédent est utilisé pour réaliser un oscillateur élastique horizontal. Tous les frottements sont négligés. On utilise un axe Ox horizontal orienté par le vecteur unitaire i et on repère la position du centre d'inertie G de la masse M, de valeur inconnue, par son abscisse x sur cet axe.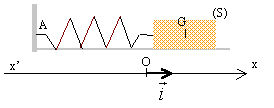

A l'équilibre ( ressort ni allongé, ni comprimé), l'abscisse x est nulle et le point G est confondu avec O. A un instant choisi comme origine des temps, la masse est écartée de sa position d'équilibre et lachée sans vitesse initiale. Le système oscille.

1. Faire un schéma des forces qui s'exercent sur la masse M.
2. En appliquant le théorème du centre d'inertie ( 2 ème loi de Newton), montrer que l'équation différentielle du mouvement peut s'écrire sous la forme : x" + w₀²x =0.
3. En déduire l'expression de la pulsation propre w₀ puis de la période propre T₀ en fonction de k et M..
4. On mesure la durée de 10 oscillations et on trouve 10,6 s. calculer T₀.
5. La masse précédente est surchargée d'une masse m = 20 g fixée sur M. Le nouveau système est mis en oscillation comme le précédent. La nouvelle durée de 10 oscillations est 10,7 s. Exprimer la nouvelle période T₁ en fonction de k, m et M.
   - En déduire l'expression de k en fonction de T₀, T₁ et m.
   - Calculer la valeur de k. Est-elle en accord avec celle trouvée par la méthode statique ?

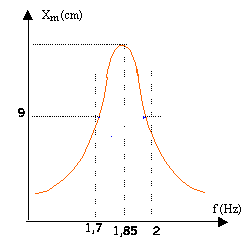
C ressort excité :

On dispose d'un système mécanique d'excitation d'amplitude constante qui permet d'imposer une fréquence d'oscillation variable N au pendule élastique. On accroche une masse M= 0,3 kg au ressort et on mesure l'amplitude notée a des oscillations pour différentes valeurs de la fréquence N.

N( Hz)	1,1	1,4	1,7	2	2,3	2,5
a (cm)	2,3	4,2	9,1	8,9	5	3,4

1. Quel est le nom du phénomène mis en évidence ? Justifier.
2. Qu'appelle-t-on fréquence propre d'un oscillateur ?
3. D'après le tableau on prend pour valeur de la fréquence propre 1,7 Hz. En déduire la valeur de k.
4. Le constructeur indique k= 39 N/m . Compte tenu des conditions expérimentales, on tolère une valeur de k comprise entre 36 et 42 N/m. Le résultat est-il satisfaisant ?
5. On se propose de trouver l'origine de cet écart et de le corriger.
   - La fréquence propre est-elle 1,7 Hz , Justifier.
   - Pour déterminer plus précisément la valeur de la fréquence propre on décide d'ajouter quelques mesures au tableau. Dans quel intervalle de fréquences est-il souhaitable de travailler. Justifier.

---

---

corrigé

---

masse m (kg)	0	0,2	0,4	0,5	0,7	1
Dl (m)	0	0,05	0,1	0,125	0,175	0,249
m / Dl	***	4	4	4	4	4

m et Dl sont proportionnels : m = 4 Dl

la masse fixée au ressort étant pseudo-isolée, tension et poids sont opposées ( principe d'inertie)

Mg = k Dl soit k = Mg /Dl = 4*9,81 = 39,2 N/m.

k : force / longueur = masse * accélération / longueur = masse *(longueur / temps²) / longueur

k : M T^-2.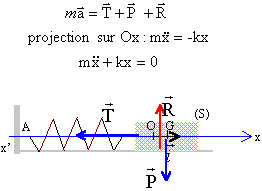

---

w₀²= k /M et T₀ = 2p(M/k)^½ = 1,06 s.

T₁ = 2p((M+m)/k)^½ = 1,07 s.

T²₀ = 4p²M / k ; T²₁ = 4p²(M+m) / k ;

T²₁ -T²₀=4p²m / k soit k = 4p²m / (T²₁ -T²₀)

k = 4*3,14²*0,02 / (1,07+1,06)*0,01) =37 N/m.

écart 5% avec la valeur précédente.

---

L'amplitude du résonateur passe par une valeur maximale lorsque la fréquence imposée par l'excitateur est comprise entre 1,7 et 2Hz : phénomène de résonance d'amplitude. ( oscillations forcées)

fréquence propre : fréquence de l'oscillateur lorsque celui-ci est en oscillation libre peu amortie.

f₀ = 1/ (2p(k/m)^½)

k = 4p²f ²₀ m= 4*3,14²*1,7²*0,3 = 34,2 N/m

ce résultat n'est pas compris dans l'intervalle [36 ; 42 ]

La fréquence propre est voisine de 1,85 Hz. Il faut faire d'autres mesures dans l'intervalle [1,7 ; 2 Hz].

---