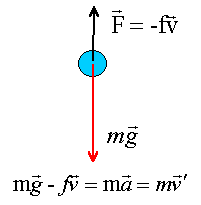Aurélie 09 /02

étude de la chute d'une goutte d'eau



Google



volume d'une sphère : 4/3 pr3.

masse volumique : de l'eau 1000 kg/m3 ; de l'air : 1,3 kg/m3.

coefficient de viscosité de l'air : h=1,81 10-5 S.I

coefficient de frottement fluide d'une sphère de rayon r se déplaçant dans l'air : f =6phr = 1,7 10-7 kg/s

rayon de la goutte d'eau supposée sphérique : r= 0,5 mm

volume de la goutte : V= 5,2 10-10 m3.masse de la goutte m= 5,2 10-7 kg.

chute libre de la goutte :

La goutte d'eau est supposée tombée dans le vide sans vitesse initiale, à partir d'un point O que l'on choisira comme origine d'un axe Ox orienté vers le bas.

  1. Etablir les équations horaires de sa vitesse v(t) et de sa trajectoire x(t).
  2. Tracer la courbe v(t) sur le graphe 2.

Pour réaliser une étude plus réaliste de la chute il faut tenir compte d'autres forces: la poussée d'Archimède et les forces de frottement.

Poussée d'Archimède : tout corps plongé dans un fluide subit une poussée verticale dirigée de bas en haut, égale au poids du fluide déplacé.

  1. Quel est le volume d'air déplacé par la goutte sphérique ?
  2. En déduire sa masse, puis le poids du volume d'air déplacé: comparer au poids de la goutte d'eau et conclure.
 

force de frottement :

La force de frottement est proportionnelle, de même direction et de sens contraire à la vitesse ( en norme F= f v). Calculer la valeur de la force F lorsque la vitesse de la goutte vaut v= 10 m/s. Comparer au poids de la goutte et conclure.

équation différentielle du mouvement de la goutte :

  1. Réaliser l'inventaire des forces s'exerçant sur la goutte en mouvement. Représenter celles-ci sur un schéma pour v= 10 m/s. ( 1 cm pour 10-6 N).
  2. La vitesse v vérifie l'équation différentielle v'= -f/m v + g. Quelle est la loi qui conduit à celle-ci ?
    - Commenter la signification physique des termes qui y figurent.
  3. La solution v(t) de l'équation différentielle est représentée par la courbe 2 (graphe 2). On peut par intégration, déterminer l'équation horaire du mouvement x(t) qui est représentée par la courbe 1 ( graphe1).
    - Evaluer l'ordre de grandeur de la distance parcourue au-delà de laquelle les frottements se font sentir de façon sensible.
    - Que devient la nature du mouvement au bout d'une dizaine de secondes ?
  4. En exploitant les courbes, déterminer la valeur vL de la vitesse limite de la goutte.
    - En exploitant l'équation différentielle déterminer l'expression de la valeur limite puis la calculer: comparer à la valeur précédente.
  5. On suppose que le rayon de la goutte est deux fois plus grand (r= 1 mm). Etudier l'influence de cette modification sur la vitesse limite de la goutte. Conclure.

 

corrigé
la goutte n'étant soumise qu'à son poids, l'accélération est verticale vers le bas, de valeur g=9,8 m/s²

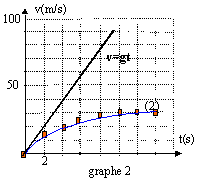
la vitesse est une primitive de l'accélération (vitesse initiale nulle) : v(t)= gt = 9,8 t.

l'altitude est une primitive de la vitesse ( altitude initiale nulle) : x(t) = ½gt² = 4,9 t².

la pousée d'Archimède due à l'air est négligeable devant le poids de la goutte d'eau car la masse volumique de l'air est très inférieure à celle de l'eau.

volume d'air déplacé = volume de la goutte d'eau = 5,2 10-10 m3.

masse de la goutte m= 5,2 10-7 kg.

poids de la goutte d'eau : mg =5,2 10-7 *9,8 =5,1 10-6 N.

poussée d'Archimède :5,2 10-10 *9,8*1,3 =6,6 10-9 N.

force de frottement fluide pour une vitesse v=10 m/s.

F=1,7 10-7 *10 = 1,7 10-6 N.

valeur du même ordre de grandeur que le poids de la goutte d'eau.

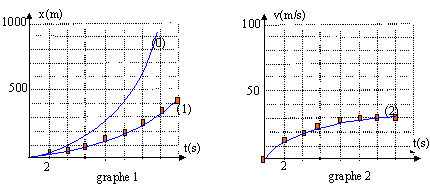
la seconde loi de Newton conduit à la relation ci-dessus.

le premier terme est le poids, le second la force de frottement fluide, le 3ème le produit de la masse de la goutte par la vitesse du centre de gravité de la goutte.

Au delà de t=2 s les il faut tenir compte des forces de frottements. la distance parcourue est de l'ordre de :

4,9 t² = 4,9*2² voisin de 20 m

au bout d'une dizaine de seconde, la goutte est pseudo-isolée (poids opposée aux frottements) et d'après le principe d'inertie le mouvement est rectiligne uniforme.

La vitesse limite , lue sur le graphe est vL=30 m/s.

d'après l'équation différentielle : v'L=0 soit -f/m vL+g=0 soit VL= mg/f.

VL= 5,2 10-7 *9,8 / 1,7 10-7 = 29,97 m/s.

le rayon de la goutte double alors :

r3 est multiplié par 8 ,donc le volume de la goutte est multiplié par 8

masse = masse volumique de l'eau * volume

donc la masse de la goutte est multipliée par 8

poids = masse *9,8 : le poids de la goutte est multiplié par 8.

par contre le coefficient de frottement fluide est proportionnelle au rayon : donc ce coefficient de frottement double.

pour une vitesse donnée, la force de frottement double.

nouvelle vitesse limite : V1 L = m1g/f1= 8mg/ (2f)= 4mg/f = 4VL.

à suivre ...
retour - menu
à bientôt ...