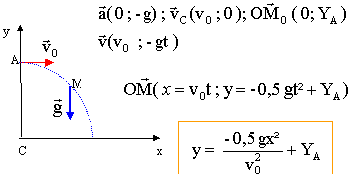|
|
||||||
|
||||||
|
|
Le bungee est un élastique composé de 960 fils de latex naturel, provenant de la sève de'hévéa, d'une section de 10 cm². Il mesure en général une dizaine de mètres. Déroulement de la séance de saut : phase 1 : la personne est attachée à un baudrier intégral fixé à l'élastique ( lui même fixé à une grue). Elle est ensuite hissée en haut de la grue à l'aide d'une nacelle qui joue le rôle d'un ascenseur. La nacelle s'élève jusqu'au point A d'altitude YA = 60 m au-dessus du sol. phase 2 : en position A, la porte de la nacelle est ouverte, il est demandé à la personne de sauter avec une faible vitesse initiale v0 de direction horizontale. Dans cette phase de saut, la personne est en chute libre jusqu'au point B' d'altitude YB'= 50 m ( ce qui signifie que l'élastique n'a aucune action sur la personne). phase 3 : après que le sauteur a passé le point B', l'élastique commence alors à s'étirer : le sauteur effectue quelques oscillations avant de s'immobiliser et d'être ramené au sol. accélération de la pesanteur g = 9,8 m/s².
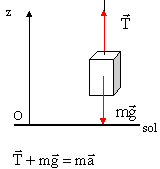
sur l'axe Oz, la 2ème loi de Newton s'écrit : T-mg= ma soit T = m( a+g). phase 1 : T1 = 270(1+9,8)= 2916 N. phase 2 : T1 = 270(0+9,8)= 2646 N. phase 3 : T3
= 270(-1,2+9,8)= 2322 N.
vitesse en B' : variation d'énergie cinétique entre les points A et B' : DEc= ½mvB'² - ½ mv0² seul le poids travaille : mg(YA-YB') le travail du poids est égal à la variation d'énergie cinétique ½mvB'² - ½ mv0² = mg(YA-YB') vB'² - v0² = 2g(YA-YB') soit vB'² = v0² + 2g(YA-YB'). vB'² =0,01 + 2*9,8( 60-50) = 196,01 soit vB' = 14 m/s. distance BB' : 50 = yB' = -4,9 x²B'/0,01 +YA. 50-60 = -490 x²B d'où xB' = 0,143 m. BB' = 0,143 m donc la chute est pratiquement verticale. oscillations libres amorties T0 = 34 / 4 = 8,5 s. T0² = 4p² m/k d'où k = 4p²m/ T0² = 4*3,14²*270 / 8,5² = 147 N/m. |
|||||
|