|
Les instruments de musique correctement accordés
produisent des notes (do5, ré5, ..., la7, si7) dont les fréquences sont
définies très rigoureusement, à savoir :
|
note
|
fréquence (Hz)
|
note
|
fréquence (Hz)
|
note
|
fréquence (Hz)
|
|
do5
|
1046
|
do6
|
2093
|
do7
|
4186
|
|
ré5
|
1175
|
ré6
|
2350
|
ré7
|
4699
|
|
mi5
|
1318
|
mi6
|
2637
|
mi7
|
5274
|
|
fa5
|
1397
|
fa6
|
2794
|
fa7
|
5588
|
|
sol5
|
1568
|
sol6
|
3136
|
sol7
|
|
|
la5
|
1760
|
la6
|
3520
|
la7
|
7040
|
|
si5
|
1976
|
si6
|
3951
|
si7
|
7902
|
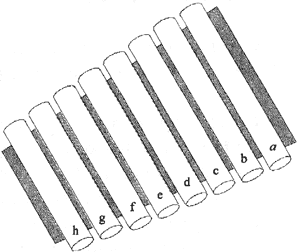
Un xylophone d'enfant est composé de 8 tubes métalliques creux (notés
a, b, ..., g, h), tous identiques mais de longueurs l
différentes. Lorsqu'on frappe sur l'un de ces tubes avec un petit
marteau, il vibre, ce qui produit un son bref d'une durée d'environ 2
secondes.
On place devant le xylophone un microphone qui transforme le
son en tension électrique. En reliant le microphone à une interface
d'acquisition, on cherche à tracer le graphe de la tension aux bornes
du microphone en fonction de la durée et à en déduire la période du son.
- Obtention de l'enregistrement.
Comme pour un oscilloscope, qu'il est nécessaire de régler, il faut
paramétrer l'interface d'acquisition afin d'obtenir un enregistrement
exploitable. On peut régler deux paramètres de la voie d'acquisition :
la durée d'acquisition (c'est-à-dire la durée de l'enregistrement) et
la sensibilité verticale (ou calibre de la voie).
L'expérimentateur fait plusieurs essais avec le tube a en utilisant un dispositif permettant de
frapper les tubes d'une façon que l'on considérera identique à chaque
fois. Il obtient les enregistrements I, II et III donnés dans l'ANNEXE
ci-dessous, représentant la tension aux bornes du microphone en
fonction de la durée.
- Quel(s) paramètre(s) de l'interface l'expérimentateur a-t-il
modifié(s) entre l'enregistrement I et l'enregistrement II ?
- Quel(s) paramètre(s) de l'interface
l'expérimentateur a-t-il modifié(s) entre l'enregistrement II et
l'enregistrement III ?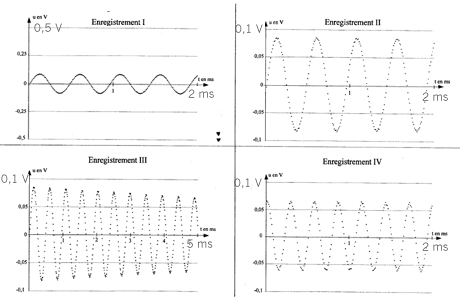
- Modélisation de la tension.
L'expérimentateur décide de conserver l'enregistrement II. Pendant la
durée d'acquisition de cet enregistrement, la tension électrique peut
être considéré comme sinusoïdale de la forme u(t) = Um cos (wt+j). Un logiciel de
traitement permet de déterminer les valeurs de Um, w et j. Pour le tube
a, il propose : Um = 83 mV ; w =
1,32 104 S.I et j = -1,74 rad.
- Le choix d'une fonction sinusoïdale comme modèle convient-il pour les
deux autres enregistrements I et III ? Justifier sans calcul.
- Que représente la grandeur Um ?
- Que représente la grandeur w ? Quelle
est son unité ?
- Donner la relation entre et la fréquence de la tension électrique.
-En déduire la valeur de la fréquence f et celle de la période T de la
tension électrique.
Aide au calcul numérique :1,32 / 2p =0,21 ; 2p /1,32 = 4,76 ; 1,32*2p
=8,29 ; 1 / (1,32*2p )= 0,121
- La vibration du tube :
On admettra que la fréquence de la vibration du tube est la même que
celle du son et que celle de la tension électrique enregistrée.
- Observation globale du phénomène : le tube vibre quand il est frappé
avec un marteau. Le son produit s'atténue et n'est plus audible au bout
de 2 secondes. Décrire par une phrase ce qui se passe pour le tube en
choisissant les termes adaptés dans la liste suivante : oscillations ;
mécaniques ; électriques ; libres ; entretenues ; forcées ; amorties ;
non amorties ; critiques.
- Etude restreinte à la durée d'acquisition : on rappelle que pendant
la durée d'acquisition de l'enregistrement, la tension électrique peut
être considérée comme sinusoïdale. Quelle est la fréquence du son émis
par le tube a ? A quelle note cela correspond-t-il ?
- L'expérimentateur a utilisé une interface d'acquisition. Il aurait pu
utiliser un oscilloscope à mémoire. Pourquoi n'a-t-il pas utilisé un
oscilloscope classique ?
- Variation de la période du son en
fonction de la longueur du tube.
On réalise la même expérience pour les 7 autres tubes. Pendant les
acquisitions, la tension électrique peut être considérée comme
sinusoïdale comme dans l'enregistrement II de la question 2. Grâce à la
valeur de donnée par le logiciel, on en déduit la période T et la
fréquence du son émis par chaque tube. On obtient le tableau de mesures
suivant :
|
Tube b
|
Tube c
|
Tube d
|
Tube e
|
Tube f
|
Tube g
|
Tube h
|
|
longueur l (cm)
|
17,3
|
16,3
|
15,4
|
14,8
|
14
|
13,2
|
12,8
|
|
T en ms
|
0,43
|
0,381
|
0,34
|
0,317
|
0,286
|
0,253
|
0,238
|
|
f en kHz
|
2,32
|
2,64
|
2,94
|
3,15
|
3,5
|
3,95
|
4
|
- On donne l'enregistrement IV dans l'annexe ci-dessus. En le comparant
aux autres enregistrements, justifier qu'il s'agit de l'enregistrement
du son d'un tube différent du tube a.
- Sans la mettre en œuvre , décrire la méthode qui permettrait de
montrer, à partir des valeurs du tableau précédent, que la période T du
son n'est pas proportionnelle à la longueur du tube ?
- On a tracé le graphe représentant T en fonction de l² :
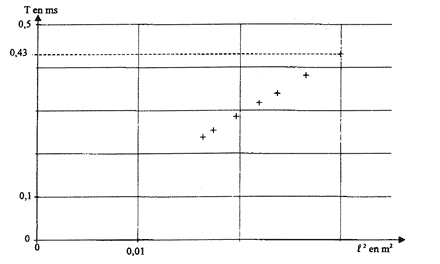
A partir du graphique, justifier que l'on peut considérer que
la période T est proportionnelle à l².
En déduire la relation numérique entre T et l en
précisant les unités.
Aide au calcul numérique : 4,3/3 = 1,4 : 3/4,3 = 0,7 ; 3*4,3 = 12,9 ;
1/ (3*4,3) = 0,078.
- Lorsque la fréquence expérimentale du son émis par un tube est très
différente de la fréquence de la note attendue pour ce tube, le tube
est mal accordé. L'expérimentateur constate que l'un des tubes est mal
accordé. Indiquer lequel.
Pour accorder ce tube, faut-il augmenter ou diminuer sa longueur, tous
les autres paramètres restant constants ? Justifier la réponse.
corrigé
Entre les enregistrements I et II seule
l'échelle de l'axe vertical a changé, donc seule la sensibilité verticale a été modifiée.
Entre les
enregistrements II et III, seule l'échelle de l'axe horizontal a
changé, donc seule la durée d'acquisition a été modifiée.
Pourl'enregistrement
I, la tension est d'amplitude constante, donc on peut la modéliser par
une sinusoïde.
Par contre, pour
l'enregistrement III, la tension a une amplitude qui décroît, donc le
choix d'une fonction sinusoïdale ne convient pas.
Um est
l'amplitude de la tension u(t) : c'est la valeur maximale prise par la
tension au cours du temps.
w est la pulsation exprimée en
rad / s.
La relation entre
la fréqence et la pulsationt est w
= 2p f.
4 périodes
correspondent à 1,9 ms : T= 4,75 10-4 s ; f= 1/T = 2100 Hz.
Le tube est le siège d'oscillations mécaniques
libres amorties
la fréquence du
son émis est la même que celle de la tension.
En regardant le
tableau au début de l'énoncé, on en déduit qu'il s'agit d'un do6.
Un oscilloscope
classique ne permet de visualiser de façon stable à l'écran que des
phénomènes qui se répètent dans le temps. Or ici deux secondes après
avoir frappé le tube, le son s'arrête, l'oscilloscope clasique n'est
donc pas adapté.
Le signal de l'enregistrement IV présente 7
périodes en 2 ms alors que les autres en présentent un peu plus de 4
pendant la même durée. Il s'agit donc bien de l'enregistrement du son
d'un tube différent du tube a.
En traçant le
graphe Cde la fonction T = f(l), on montrerait que la période du
son n'est pas proportionnelle à la longueur du tube car C ne serait pas
une droite passant par l'origine du repère.
Le graphe de la
fonction T= f (l²) est une droite passant par l'origine du
repère donc on peut considérer que T est T proportionnelle à l²
.
La droite passe
par le point de coordonnées ( 0,03 m² = 3 10-2 m²; 0,43 ms =
4,3 10-4 s) donc le coefficient de proportionnalité est :
a = 4,3 10-4
/ 3 10-2 = 1,4 10-2 s m-2.
Donc T= 1,4 10-2
l² avec l en m et T en s.
le tube a
correspond au do6. Le tube d devrait correspondre au fa6, c'est-à-dire
osciller à une fréquence voisine de 2794 Hz ; or il oscille à 2940 Hz.
C'est donc le tube d qui est ma accordé.
Comme il y a
proportionnalité entre T et l² pour diminuer la fréquence du
son émis, il faut augmenter sa période, c'est à dire augmenter la
longueur du tube.
|


