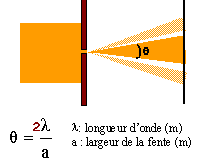Aurélie 05/02

dispersion par un prisme ; diffraction



Google



dispersion par un prisme :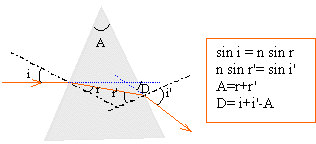

 Un prisme de verre d'indice n a pour section droite un triangle d'angle au sommet A=60°.

  1. En prenant l'indice de l'air égal à 1 et celui du verre à n, rappeler les relations entre i et r d'une part et i' et r' d'autre part.
  2. Le verre constituant le prisme est un milieu dispersif. Donner la définition du phénomène de dispersion.
    - Dans le prisme la longueur d'onde d'une radiation donnée est-t-elle différente de sa longueur d'onde dans l'air ? Quelle est la grandeur qui se conserve ?
  3. Un rayon lumineux, transportant une longueur d'onde dans le vide l1=435,9 nm arrive de l'air sur la surface du prisme d'indice n1= 1,668. L'angle d'incidence est i = 56,0°. Calculer les valeurs des angles r, r' , i' et D1.
  4. Un rayon lumineux composé de trois radiations de longueur d'onde dans le vide l1=435,9 nm, l2=546,1 nm, l3=646 nm arrive de l'air sur la surface du prisme constitué d'un verre dont les indice sont respectivement n1= 1,668 , n2= 1,654, n3= 1,640. L'angle d'incidence est i = 56,0°.
    - Quelle est la couleur de chacune de ces trois radiations ?
    - Calculer les déviations D2 et D3.
    - Indiquer sur un schéma quelle est la radiation la plus déviée et quelle est la moins déviée.
    - Calculer l'écart angulaire a entre la radiation la plus déviée et la moins déviée.
 

corrigé
sin i = n sin r et n sin r' = sin i'

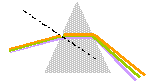
dispersion de la lumière par un prisme :

après avoir traversé le prisme de verre, les différentes radiations colorées constituant la lumière blanche sont déviées différemment ; dans le prisme les vitesses de propagation sont différnetes pour des radiations de fréquences différentes.

La longueur d'onde d'une radiation de fréquence donnée dépend du milieu de propagation :

dans le prisme la longueur d'onde d'une radiation donnée est égale à la longueur d'onde dans le vide divisée par l'indice de réfraction n.

l verre = l vide / n

C'est la fréquence de la radiation qui se conserve.

sin r = sin 56 / 1,668 d'où r = 29,8°.

A= r + r' d'où r' = 60 - 29,8 = 30,2°.

sin i' = n sin r' = 1,668 * sin 30,2 d'où i' = 57,03°.

déviation D1 = i + i ' -A = 56 + 57,03 -60 = 53,03°.

l1=435,9 nm (bleu violet) ; l2=546,1 nm ( vert) ; l3=646 nm ( jaune)

pour la seconde radiation, un calcul identique donne :

r = 30,08° ; r' = 29,92°, i' = 55,58° et D2 = 51,58°.

pour la troisième radiation :

r = 30,37° ; r' = 29,63°, i' = 54,19° et D3 = 50,19°.

la radiation bleu est la plus déviée

écart angulaire a = D1-D3 = 53,03 - 50,19 = 2,86°.


diffraction :

Le schéma ci-dessous est une reproduction de la figure de diffraction obtenue sur un écran situé à 2m d'une fente de largeur 100 mm, éclairée par une lumière émise par une diode laser.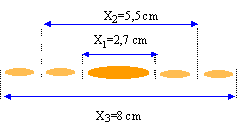

 

  1. Quelle relation existe-t-il entre le demi-diamètre angulaire q de la tache centrale de diffraction, la longueur d'onde l et la largeur de la fente a ?
  2. Etablir la relation entre la largeur a de la fente, tan q ,la largeur X1 de la tache centrale de diffraction et la distance D séparant l'écran de la fente.
    - Simplifier cette relation si q est petit.
    - Déterminer la longueur d'onde l dans le vide de la lumière émise par la diode laser.
  3. Quelle particularité de la figure de diffraction les mesures permettent-elles de mettre en évidence.
  4. En utilisant le même dispositif :
    - Quelle serait la dimension de la tache centrale obtenue avec une lumière monochromatique bleue de longueur d'onde 450 nm.
    - Décrire l'aspect de la tache centrale de diffraction obtenue avec une lumière blanche.
 

corrigé

tan (½q) = ½X1 / D et si q est petit ½q = ½X1 / D soit q (radian) = X1 / D

X1 / D = 2l/a d'où l = a X1 / (2D)

l =10-4 *2,7 10-2 / (2*2) = 0,675 10-6 m = 675 nm.

On remarque que X2 = 2X1 et que X3 = 3 X1.

X1 / D = 2l/a d'où X1 = 2Dl/a

X1 = 2*2 *4,5 10-7 / 10-4= 1,8 cm.

En lumière blanche on observe une tache centrale blanche et bordée de rouge :

au centre toutes les radiations sont présentes

la tache rouge est plus large que les autres et déborde.


à suivre ...
retour - menu
à bientôt ...