|
On considère un ressort à spires non jointives d'axe
horizontal, de raideur k. L'extrémité A du ressort est fixe. Un solide
S, de masse m = 250 g, est accroché à l'autre extrémité du ressort et
se déplace sans frottement sur un banc à coussin d'air horizontal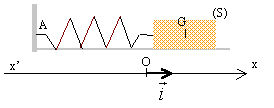
La masse du ressort est négligeable devant m. On étudie le
mouvement du centre d'inertie G du solide, dans le référentiel du
laboratoire considéré comme galiléen. On repère la position de G par
son abscisse x sur un axe horizontal x'x d'origine O :
le point O correspond à la projection de la position de G à
l'équilibre.
Etude théorique :
- En appliquant le théorême du centre d'inertie, établir
l'équation différentielle admettant x(t) comme solution.
- En déduire l'expression de la pulsation propre w0 en fonction des caractéristiques de
l'oscillateur.
- Une solution de l'équation différentielle précédente peut
être écrite sous la forme : x(t) = Xm cos( 2p/T0 t + j )
dans laquelle Xm est l'amplitude du mouvement et j la phase à l'origine des dates.
- En déduire l'expression littérale de la coordonnée vx du
vecteur vitesse du point G en fonction du temps.
-Donner les expressions littérales de l'abscisse x(0) et de la
coordonnée vx(0) à l'origine des dates, en fonction de Xm,
T0 et j.
Etude expérimentale :
Deux expériences notées 1 et 2 ont été réalisées, avec le même
solide S. Pour chaque expérience, l'origine des dates coïncide avec
l'instant où le solide S est abandonné ou lancé, après avoir été écarté
de sa position d'équilibre. A chaque expérience correspond un
enregistrement ; les figures ci dessous donnent les variations de x en
focntion du temps t. Le numéro de la figure est identique à celui de
l'expérience.
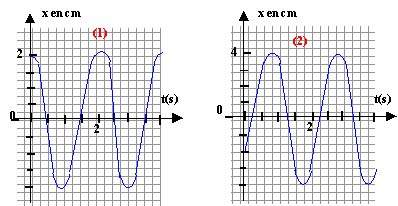
- A partir des enregistrements des figures 1 et 2, traiter
sans justification, les questions ci-dessous en reportant les réponses
dans le tableau ci dessous :
|
expérience
|
1
|
2
|
|
T0
|
.....................
|
.......................
|
|
Xm
|
|
|
|
x(0)
|
|
|
|
vx(0)
|
|
|
|
ressort
|
|
|
- Déterminer les valeurs de T0, Xm et x(0).
- Déterminer si vx(0) est nulle, positive ou négative.
- Parmi les termes suivants, choisir, sans justification, ceux qui
décrivent les conditions initiales relatives au ressort : comprimé,
étiré ou non déformé.
- Justifier que l'enregistrement de la figure 2 ci-dessus a
été obtenu en utilisant le même ressort que celui de l'expérience 1.
- On désigne par Em l'énergie mécanique du système
{ressort + solide + Terre} (système encore noté {ressort + solide} dans
le champ de pesanteur). L'énergie potentielle de pesanteur est choisie
nulle dans le plan horizontal passant par G.
- Etablir l'expression littérale de Em en fonction de
l'amplitude Xm.
- On désigne par Em1 et Em2 l'énergie mécanique
du système respectivement pour les expériences 1 et 2. Parmi les
propositions suivantes, choisir, en justifiant, celle qui convient : Em2
/ Em1 =1 ; Em2 / Em1 =2 ; Em2
/ Em1 =4
- Comparer, sans les calculer numériquement, les énergie
potentielles élastiques Ep1(0) et Ep2(0) du
système {ressort + solide + Terre} à la date t0 = 0 s pour
ces deux enregistrements. Justifier la réponse.
corrigé
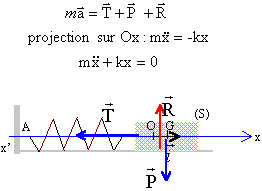 avec w0²
= k/m avec w0²
= k/m
vitesse : dérivée
de l'abscisse par rapport au temps
x(t) = Xm cos( 2p/T0
t + j )
vx(t)
= - Xm 2p/T0 sin(
2p/T0 t + j )
x(0) = Xm cos( j )
vx(0)
= - Xm 2p/T0 sin(
+ j )
|
expérience
|
1
|
2
|
|
T0
|
2 s
|
2 s
|
|
Xm
|
2 cm
|
4 cm
|
|
x(0)
|
2 cm
|
-2 cm
|
|
vx(0)
|
0
|
positive
|
|
ressort
|
étiré
|
comprimé
|
les deux enregistrements ont été effectués avec le même système
{ressort + masse }car la période est la même : la période ne dépend que
de la raideur du ressort et de la masse accrochée à ce ressort. Par
contre les conditions initiales étaient différentes.
énergie mécanique = énergie potentielle + énergie cinétique
Em = ½kx² + ½mv²
Em = ½kX²m cos²( 2p/T0
t + j ) + ½m X²m [2p/T0
]² sin²( 2p/T0 t + j )
or m [2p/T0 ]² = m w0² = k
Em = ½kX²m cos²( 2p/T0
t + j ) + ½ k X²m sin²( 2p/T0 t + j )
Em = ½kX²m [cos²( 2p/T0
t + j ) +sin²( 2p/T0
t + j )]=½kX²m.
l'amplitude Xm2 ( expérience 2) est le double de
l'amplitude Xm1 ( expérience 1) l'énergie mécanique est
proportionnelle au carré de l'amplitude : donc Em2
/ Em1 =4.
l'énergie potentielle est proportionnelle au carré de
l'abscisse : Ep = ½kx²
or à t=0 , dans les deux expériences l'abscisse initiale a
même valeur absolue : |x1(0) |= |x2(0) | =0,02 m
donc Ep1(0) = Ep2(0).
|


 avec w0²
= k/m
avec w0²
= k/m