Aurélie 05/02

charge et décharge d'un condensateur

Pondichéry 04/ 02


Google



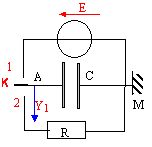
Rappel :

La tension aux bornes d'un condensateur chargé à travers un résistor R par une source de tension constante atteint 63% de sa valeur maximale au bout d'un temps t = RC.

La tension aux bornes d'un condensateur qui se décharge à travers un résistor R a diminué de 63% de sa valeur maximale au bout d'un temps t = RC.( constante de temps du dipôle RC)

partie 1 :

On réalise le montage suivant comportant un générateur de f.e.m E= 9V et de résistance interne négligeable, un condensateur dont la capacité varie entre 40 et 80 mF, un conducteur ohmique de résistance R= 10 ohms.

I. Le condensateur est préalablement déchargé.

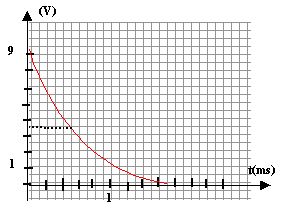
  1. Quel est le phénomène physique mis en jeu quand on place l'interrupteur K en position (1) ?
  2. Pourquoi ce phénomène est-il très rapide ?

II. Un ordinateur muni d'une carte d'acquisition permet d'enregistrer l'évolution au cours du temps de la tension uAM entre les bornes du condensateur. L'acquisition des données commence lorsqu'on bascule l'interrupteur K de la position (1) à la position (2). La courbe obtenue est la suivante :

  1. Quel est le phénomène physique mis en évidence ?
  2. En utilisant la courbe donnée déterminer une valeur approchée de la capacité du condensateur.
  3. On reprend la même expérience avec un condensateur de capacité 2 fois plus grande. Donner sur la figure précédente l'allure de la courbe obtenue . Justifier.

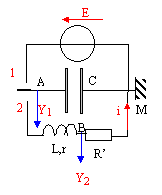
partie 2 :

 On réalise le montage suivant comportant un générateur de f.e.m E= 9V et de résistance interne négligeable, un condensateur dont la capacité varie entre 40 et 80 mF, un conducteur ohmique de résistance R'= 5 ohms, une bobine d'inductance L= 1H et de résistance r = 10 ohms.

L'interrupteur K est placé en position (1) puis basculé en position (2). L'acquisition des données commence lorsqu'on bascule l'interrupteur K de la position (1) à la position (2).

  1. Quelles sont les grandeurs visualisées en voies Y1 et Y2 ?
    - L'une de ces grandeurs permet de connaître les variations de l'intensité i du courant Laquelle ? Justifier.
  2. Les grandeurs visualisées sont représentées sur la figure ci-dessous :

    - Associer les courbes x et y aux voies Y1 et Y2 .
    - Quel est le phénomène observé ?
    - Pourquoi ne se produit-il pas dans l'expérience précédente ?

  3. La figure ci-dessous représente les variations au cours du temps de l'énergie EE emmagasinée par le condensateur, de l'énergie EM emmagasinée par la bobine et leur somme E.

    - Donner les expressions littérales des énergies EE et EM.
    - Identifier les 3 courbes en justifiant.
    - En comparant lex courbes 3 et 4 donner une interprétation du phénomène étudié.
    - Interprèter qualitativement l'évolution de l'énergie représentée par la courbe (5).
    - Evaluer l'énergie dissipée pendant les 60 premières millisecondes.

 

corrigé
Quand l'interrupteur passe en position (1) le condensateur est relié à un générateur de tension continue : le condensateur va se charger. La tension aux bornes du condensateur va augmenter jusqu' à atteindre 9 V en fin de charge. les armature se différencient et portent des charges opposées.

Le phénomène est d'autant plus rapide que la constante de temps RC est petite. Ici R est voisin de zéro et C voisin de 6 10-6 F. La charge est terminée au bout d'une durée voisine de 5 fois RC

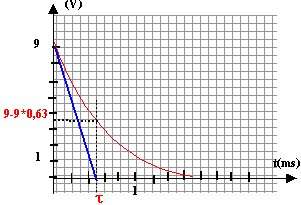
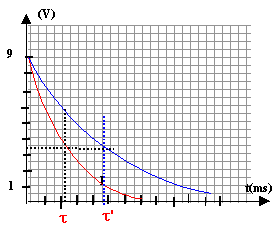
Le condensateur chargé est relié à un résistor : on observe la décharge du condensateur à travers le résistor.

t voisin de 0,5 ms = 5 10-4 s

5 10-4 = 10 C d'où c vosin de 5 10-5 F soit 50 mF.

si la capacité double la constante de temps double : la valeur 9-9*0,63 = 3,5 V est atteinte au bout d'un temps deux fois plus grand.

partie 2 :

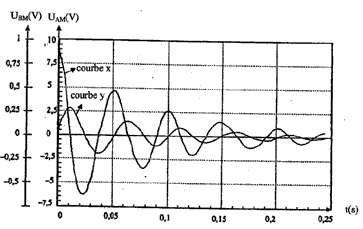
Sur la voie 1 on visualise la tension aux bornes du condensateur UAM.

Sur la voie 2 on visualise la tension aux bornes du résistor UBM.

La tension aux bornes d'un résistor et l'intensité sont proportionnelles : donc la tension UBM permet de connaître l'intensité au facteur R= 5 près .

A l'instant t= 0 la tension aux bornes du condensateur est maximale et vaut 9V: la courbe x correspond donc à UAM.

A l'instant t= 0 l'intensité dans le circuit est nulle : la courbe y correspond à la tension UBM.

Le condensateur se décharge à travers la bobine inductive : on observe un échange permanent d'énergie entre le condensateur et la bobine. Une partie de l'énergie est dissipée par effet joule dans les résistances.

oscillations élelectriques libres et amorties.

Dans l'expérience précédente ( partie 1) on n'observe pas ce phénomène car il n'y a pas de bobine inductive.

énergies :

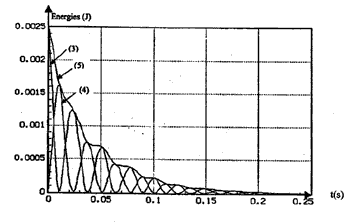
énergie stockée par le condensateur : EE = ½ CU²

à l'instant t=0, le condensateur chargé n'a pas encore eu le temps de se déchargé et en conséquence il emmagasine toute l'énergie du dipole RLC : donc courbe(3)

énergie stockée par la bobine : EM =½Li².

à t = 0 l'intensité du courant étant nulle, la bobine n'emmagasine aucune énergie donc courbe (4)

la courbe (5) correspond à la somme E= EE + EM.

du fait de l'amortissement ( dissipation d'énergie dans les résistances par effet Joule) l'énergie emmagasinée par le dipole RLC diminue au cours du temps.

à t = 0 , E = 2,5 mJ et à t = 0,06 s E voisine de 0,4 mJ

énergie perdue voisine de 2,1 mJ.



à suivre ...
retour - menu
à bientôt ...