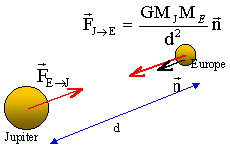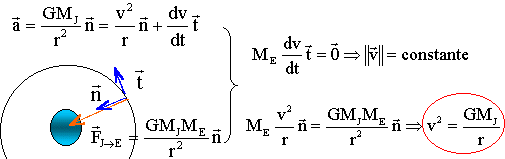Données :

Galilée commença à observer la planète Jupiter en janvier 1610 avec une lunette de sa fabrication. Il découvrit qu'autour de Jupiter tournaient quatre lunes auquelles il donna le nom d'astres médicéens; ce sont quatre satellites de Jupiter : Io, Europe, Ganymène et Callisto.

G constante de gravitation universelle = 6,67 10^-11 SI

masse de Jupiter M_J = 1,9 10²⁷ kg ; rayon de Jupiter R_J= 7,15 10⁴ km ;

période de rotation de Jupiter sur elle même : T_J= 9 h 55 min

Masse du satellite Europe (noté E) : M_E ; Rayon de l'orbite du satellite Europe : r_E= 6,7 10⁵ km

Période de révolution du satellite Europe autour de Jupiter : T_E= 3 j 13 h 14 min.

Tous les corps seront supposés à répartition de masse à symétrie sphérique et on supposera que chaque satellite n'est soumis qu'à l'influence de Jupiter.

partie 1 : les vecteurs sont notés en bleu et en gras.

1. Représenter sur un schéma la force de gravitation F _J-->E exercée par Jupiter sur Europe et celle F_E-->J exercée par Europe sur Jupiter.
   - Donner l'expression vectorielle de F _J-->E , les centres des deux astres étant séparés d'une distance d.
2. Définir un mouvement uniforme.
   - Le mouvement du satellite Europe ( noté E) est étudié dans le référentiel " jupiterocentrique". Par analogie avec le référentiel géocentrique, donner les caractéristiques d'un référentiel jupiterocentrique.
   - Montrer que le mouvement du satellite Europe en orbite circulaire est uniforme dans le référentiel jupiterocentrique.
   - Comparer les vecteurs vitesses V₁ et V₂ et les vecteurs accélération a₁ et a ₂ du satellite aux points E₁ et E₂.
   - Représenter ces vecteurs.

partie 2 :

1. Etablir que la valeur de la vitesse du satellite de Jupiter est V² = GM_J / r où r désigne le rayon de l'orbite du satellite.
2. En déduire l'expression de la période T de révolution du satellite en fonction de G, M_J et r.
3. Montrer que le rapport T² / r³ est constant pour les différents satellites de Jupiter. ( ce résultat correspond à la troisième loi de Kepler).
   - La période de révolution de Io autour de Jupiter est T_Io = 1 j 18 h 18 min. Thébé, un autre satellite de Jupiter, possède une orbite de rayon moitié de l'orbite de Io. Déterminer la période de révolution T_th de Thébé autour de Jupiter.
4. Par analogie avec la définition d'un satellite géostationnaire, un satellite jupiterostationnaire est un satellite fixe par rapport à Jupiter. Europe est-il jupiterostationnaire ? Justifier sans calculs à l'aide des données.

---

---

corrigé

---

---

mouvement uniforme : la norme du vecteur vitesse est constante.

Un référentiel Jupiterocentrique est centré sur Jupiter et les trois axes pointent vers des étoiles lointaines qui paraissent fixes.

Ecrire la 2 ème loi de Newton dans la base de Frenet :

Europe n'est soumis qu'à la force de gravitation attractive exercée par Jupiter et dirigée vers le centre de Jupiter ( pas de composante tangentielle)

---

satellite aux points E₁ et E₂ :

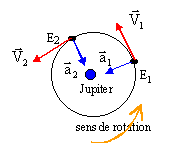
Les vecteurs vitesses V₁ et V₂ ( V² = GM_J/ r) ont même norme mais des directions différentes

Les vecteurs accélération a₁ et a ₂ ( a = V² / r) ont même norme mais des directions différentes

---

période de révolution T :

durant une période T le satellite décrit une circonférence de rayon r à vitesse constante V :

2pr = V T soit 4p² r² = V² T²

remplacer V² par GM_J/ r d'où : 4p² r² = GM_J/ r T²

soit T² / r³ = 4p² / (GM_J) rapport constant pour une planète donnée.

T²_Io / R³_Io = T²_Th / R³ _Th soit T²_Th =T²_Io R³ _Th / R³_Io .

R³ _Th / R³_Io = (0,5 R_Io )³ / R³_Io = 0,5³ = 0,125

T²_Th = 0,125 T²_Io soit T_Th = 0,354 T_Io

mettre T_Io en minutes : 24*60 +18*60+18 = 2538 min

T_Th = 0,354*2538 = 896 min = 14 h 56 min.

---

jupiterostationnaire :

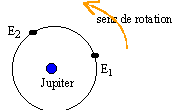
un satellite juputérostationnaire doit se trouver dans le plan équatorial de Jupiter

il doit tourner dans le même sens que Jupiter

sa période doit être égale à celle de Jupiter

T_E est différent de T_J : donc Europe n'est pas jupiterostationnaire.

---