Aurélie 03/02

étincelle de rupture

Liban 06/01


Google



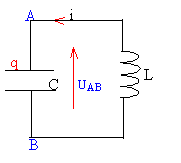
étude d'un circuit L, C :

On considère le circuit idéal comportant un condensateur de capacité C et une bobine d'inductance L, de résistance négligeable. On appelle q(t) la charge portée par l'armature A à la date t.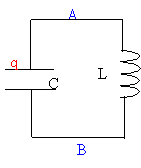

 

  1. En exprimant la tension aux bornes de chaque dipôle, montrer que q eqt une fonction du temps obéissant à l'équation différentielle : q" + 1/(LC) q = 0.
  2. Les solutions de cette équation différentielle sont de la forme : q(t) = Q cos (w0t + j ) avec Q >0 et w0 et j grandeurs indépendantes du temps. A la date t= 0 l'armature A du condensateur porte la charge Q0 >0 et l'intensité du courant est nulle. Déterminer les expresssions littérales de Q, w0 et j.
  3. Sous quelle forme l'énergie est-ele emmagasinée dans le circuit à la date t=0. Décrire rapidement ce qu'elle devient par la suite.
    - En réalité une bobine possède toujours une résistance interne. Quelle en est la conséquence sur l'énergie ?

Une application de ce type d'association :

On considère le circuit (1) constitué d'une source de tension continue de f.e.m E, d'un conducteur ohmique de résistance R, d'un interrupteur K fermé et d'une bobine d'inductance L, de résistance interne négligeable.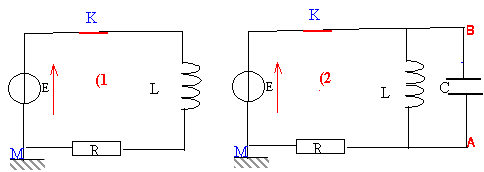

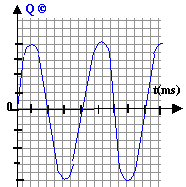
  1. On admet qu'au bout d'un temps suffisamment long on atteint un régime permanent pour lequel l'intensité du courant est constante. Montrer que l'intensite est I= E/R.
  2. A l'ouverture de K, si la valeur de l'intensité et de l'inductance sont suffisamment grandes, on observe une étincelle de rupture au niveau de l'interrupteur. Quel phénomène est responsable de cette étincelle ?
  3. On complète le circuit en ajoutant un condensateur aux bornes de la bobine ( circuit (2) ). l'interrupteur K étant fermé, montrer qu'en régime permanent l'intensité du courant circulant dans la bobine a toujours la même valeur I= E/ R et que la tension aux bornes du condensateur est nulle.
    - On ouvre à nouveau l'interrupteur. Pourquoi n'y a t-il plus d'étincelle ?
    - Dessiner l'allure du graphe de la charge q(t) après l'ouverture de K. Déterminer la valeur maximale de cette charge.

 

corrigé
équation différentielle :

tension aux bornes de la bobine : UBA = L di / dt

tension aux bornes du condensateur : UAB = q / C

avec i = dq/ dt = q ' et i' = di / dt = q"

UBA+ UAB = 0

L di / dt + q / C = 0

Lq" + q/ C=0

q" + w0² q = 0 avec w0² = 1 / LC.

q(t) = Q cos (w0t + j )

intensité i = q' = -Qw0sin (w0t + j )

à t = 0 l'intensité est nulle : 0 = -Qw0sin (0 + j )

Qw0 n'est pas nul donc sin ( j ) =0 soit j = 0 ou j= p.

à t = 0 : q =Q0 = Q cos (0 + j )

si j = 0 alors Q0 = Q.

si j= p alors Q0 = - Q

on ne retient pas cette solution car Q est positif.

énergie :

à la date t = 0 l'énergie est stockée dans le condensateur : E (t=0 ) ½ Q0² / C

puis il y a un échange permanent d'énergie entre la bobine et le condensateur.

Au cours de ces échanges une partie de l'énergie est perdue dans la résistance de la bobine sous forme d'effet joule ( r i ² t)

on parle d'amortissement des oscillations.

étincelle de rupture (circuit 1):

phénomène d'autoinduction.

on observe un retard à l'établissement du courant à la fermeture de l'interrupteur.

Ce retard est du au fait que la bobine stocke de l'énergie : ½ Li².

La tension aux bornes de la bobine est : U = L di / dt + ri

si l'intensité est constante ( régime permanent )U = r i voisin de zéro si r est négligeable

en conséquence Ri = E soit i = E/R.

à l'ouverture de l'interrupteur la bobine restitue l'énergie préalablement stockée ( d'où l'étincelle aux bornes de K)

pas d'étincelle de rupture (circuit 2):

en régime permanent la tension aux bornes de la bobine est voisine de zéro si la résistance de la bobine est négligeable.

or le condensateur et la bobine sont en dérivation : donc la tension aux bornes du condensateur est égale à la tension aux bornes de la bobine soit zéro.

tension aux bornes du condensateur et charge des armatures sont proportionnelles : la charge du condensateur est donc nulle.

l'intensité en régime permanent vaut toujoirs i = E / R.

à l'ouverture de l'interrupteur il y a échange d'énergie entre condensateur et bobine : en conséquence pas d'étincelle aux bornes de l'interrupteur.

charge du condensateur en fonction du temps ( si résistance négligeable )

 

énergie maximale stockée dans la bobine ½ Li² = ½L E² / R²

énergie maximale stockée dans le condensateur : ½ Q² / C

½L E² / R² = ½ Q² / C

d'où : LC E² / R² = Q²



à suivre ...
retour - menu
à bientôt ...