Aurélie 02/02

pendule sur un plan incliné



Google



Un pendule pesant simple de longueur L est constitué d'un mobile autoporteur de masse m fixé à un fil inextensible. Il se déplace sur une table inclinée d'un angle a par rapport au plan horizontal. Les frottements sont négligés.

On prendra l'énergie potentielle de pesanteur nulle pour la position d'équilibre du pendule (position A).

  1. Décrire la trajectoire suivie par le centre d'inertie du pendule en oscillations.
  2. On écarte le pendule de sa position d'équilibre d'un angle q0. Exprimer son énergie potentielle de pesanteur en B.
  3. On abandonne le pendule sans vitesse initiale. Exprimer sa vitesse lors de son passage par la position d'équilibre en A.
  4. Exprimer l'énergie mécanique du pendule en fonction de q, écart angulaire à l'instant t (par rapport à OA) et sa dérivée par rapport au temps (dq/dt = q ') dans le cas de petites oscillations. (sin q voisin de q en radian).
  5. Etablir à partir de l'énergie mécanique l'équation différentielle du mouvement du centre de gravité G et en déduire l'expression de la période T.
  6. Calculer sin a pour que cette période soit celle d'un pendule simple, de même longueur L, oscillant sur la lune dans un plan vertical.

donnée : gTerre/gLune= 6.

 

 

corrigé

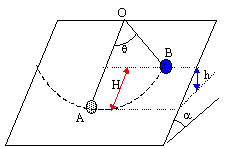
trajectoire de la masse fixée au fil : un arc de cercle de rayon L, de centre O.

énergie potentielle de pesanteur : mgh

différence d'altitude entre A et B notée h : h = H sin a.

H = OA -OBcosq = OA (1- cosq)

h = L(1- cos q ) sin a.

énergie potentielle de pesanteur : mgh = mgL(1- cos q ) sin a.

vitesse en A :

au passage à la position d'équilibre en A l'énergie est sous forme cinétique : 0,5 m v²

l'énergie mécanique se conserve : 0,5 mv² = mgh

d'où v² = 2gh = 2 g L(1- cos q ) sin a.

énergie mécanique pour une position quelconque :

somme de l'énergie cinétique et de l'énergie potentielle de pesanteur

0,5 m v² + mgh = Cte

0,5 m v² + L (1- cosq) sin a = Cte

avec q ' L = v et sin a une constante

équation différentielle du mouvement :

dériver par rapport au temps l'expression de l'énergie mécanique

0,5 m *2 v v' + mgL sin q q ' sina = 0

tout diviser par la masse m : v v' + gL sin q q 'sin a = 0

remplacer v par : q ' L

Lq' v' + gL sin q q ' sin a =0

diviser par Lq '' : v' + g sin q sina =0

remplacer v' par : q " L

L q " + g sin q sin a = 0

si q petit ( petites oscillations) sin q voisin de q radian

L q " + g q sina = 0

q " + g sina /L q =0

w ² = g sina /L

w ² = 4 p ² / T²

T = 2 p racine carrée ( L / (g sin x))

pendule simple oscillant sur la lune : T = 2 p rac. carrée ( 6L/gTerre)

les périodes et les longueurs L sont égales donc 1 / sin a = 6 et sin a = 1/6.

 



à suivre ...
retour - menu
à bientôt ...