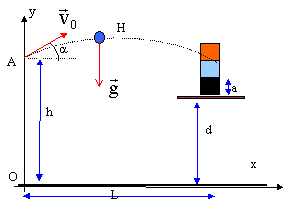
Dans tout l'exercice, on ne tiendra pas compte de la résistance de l'air, et on considérera la balle comme ponctuelle. On prendra g = 10 m/s².

Un enfant participe à un jeu de chamboule-tout qui consista en projetant une balle sur un empilement de boites à faire tomber le maximum de boites.On supposera dans l'exercice que toute boite touchée et celles qui sont au-dessus tomberont.

Pour effectuer son lancer l'enfant tend son bras vers le haut à une distance h = 1, 80 m au-dessus du sol. La balle part avec une vitesse v₀ de valeur v₀= 10 ms^-1 faisant un angle a = 12 ° vers le haut avec l'horizontale.

Trois boites sont empilées les unes au-dessus des autres sur un support s'élevant à une hauteur d = 1, 55 m du sol. La plus grande distance entreles boîtes et la verticale passant par A est L = 4 m. Chaque boîte a une hauteur a = 10 cm.

1. Etablir les équations paramétriques du mouvement de la balle dans le repère ( O , i , j ) en choisissant l'instant de départ de la balle comme instant d'origine ( O étant le point du sol horizontal appartenant à la verticale passant par A )
2. Donner l'équation de la trajectoire de la balle.
3. Calculer les coordonnées du point H ; hauteur maximale atteinte par la balle.
4. Combien de boites seront renversées au cours de cet essai ?
5. En utilisant le théorème de l'énergie cinétique, exprimer la valeur de la vitesse V_M de la balle au point d'impact M en fonction de v₀ , g , h , d et a.

---

---

corrigé

---

accélération ( 0, -g)

vitesse initiale ( v₀ cos a ; v₀ sin a )

position initiale : (0 ; h)

la vitesse est une primitive de l'accélération ( v₀ cos a ; -gt + v₀ sin a)

le vecteur position est une primitive de la vitesse :

x = v₀ cos a t ; y = -½ g t² + v₀ sin a t + h

---

trajectoire :

t = x / v₀ cos a repport dans y

y = - ½ gx² / (v₀ cos a)² + x tan a + h.

---

hauteur maxi :

en H, point le plus haut, la vitesse est horizontale

soit -gt + v₀ sin a =0 ou t = v₀ sin a / g

repport dans y = -0,5 gt² + v₀ sin a t + h

Y max = -0,5 g (v₀ sin a)² / g² + (v₀ sin a )² / g + h

Y max = 0,5 (v₀ sin a)² / g + h

quand à X max remplacer t par v₀ sin a / g dans x(t) :

X max = v₀ cos a v₀ sin a / g = v₀² sin a cos a / g

---

combien de boîtes? :

distance des boîtes L= 4 m

calculer l'altitude pour x = 4

y = -5 * x² / (10 cos 12 )² + x tan 12 + 1,8

y = -0,052 x² + 0,212 x +1,8

puis remplacer x par 4

y = -0,832 + 0,848 +1,8 = 1,816 m

hauteur de la 3ème boîte : 1,55 + 0,3 = 1,85 m

de la seconde 1,75 m

la 3ème boîte est touchée et tombe.

---

th de l'énergie cinétique :

état initial A avec v= v₀ et h = 1,8 m

état final 3ème boîte touchée vitesse V_M et h = d + 3 a ( a = 0,1)

travail du poids : mg (h-d-3a)

variation énergie cinétique : ½mV²_M- ½mv₀²

V²_M - v₀² = 2g(h-d-3a)