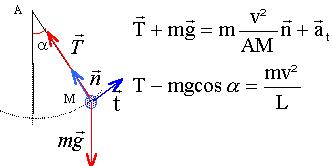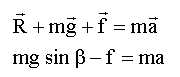Aurélie 01/02

divers mouvements



Google



  1. Observer les figures ci-dessous. Pour chaque cas, préciser si le solide S est pseudo-isolé ou non en justifiant.
  2. Deux pierres de masses identiques sont lancées du haut d'une falaise : l'une est lancée vers le haut, l'autre vers le bas. Comparer le travail du poids de chaque pierre, au cours de leur chute jusqu'au sol supposé horizontal ; justifier.

Les deux parties sont indépendantes.

  1. Un solide ponctuel de masse m est attaché à l'extrémité d'un fil de longueur L. L'extrémité A du fil étant fixe, on lance le solide à partir du point H de manière à lui imposer un mouvement circulaire autour de A dans un plan vertical. La position M du solide au cours de son mouvement est repérée par l'angle a = (AH,AM).

    - A l'aide de la relation fondamentale de la dynamique, montrer que le mouvement n'est pas uniforme.
    - Montrer que la tension du fil vérifie la relation : T = mg cos    a + mw ²L (w vitesse angulaire du solide).
    - En déduire la valeur minimale de la vitesse VH', au point culminant H' atteint par le solide, pour que le fil reste tendu.
    Données : m = 100g ; L = 40cm ; g = 9,8N.kg-1.

  2. Le solide est libéré de son attache lorsqu'il passe en montant par le point O, il tombe alors sur un plan incliné, avec lequel il entre en contact au point I avec une vitesse Vi. Le plan est rugueux, les frottements peuvent être assimilés à une force de valeur f constante.
    - Déterminer l'accélération prise par le solide.
    - Déterminer sa vitesse lorsqu'il arrive en J.
    - Calculer la durée du parcours IJ.
    Données : Vi = 4,4 m.s-1 ; f = 0,50 N ; IJ =d = 2,0 m ; b= 20°.

corrigé


 

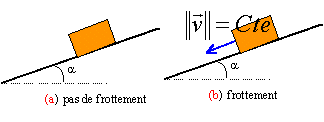
a : le bloc descend le plan à vitesse croissante en absence de frottement ; la somme des forces n'est pas nulle et le solide n'est pas pseudo isolé

b : mouvement rectiligne uniforme (norme de la vitesse constante) donc solide pseudo isolé d'après le principe d'inertie.

le travail d'une force constante comme le poids ne dépend pas du chemin suivi mais uniquement des positions de départ et d'arrivée.

le travail du poids est identique si les pierres sont la même masse.

le solide est soumis à son poids et à la tension du fil : la somme vectorielle de ces deux forces n'est pas nulle.

donc le mouvement n'est pas uniforme et il y a une accélération.

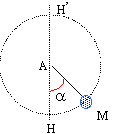
utiliser la base de Frenet et projeter les forces sur l'axe n :

T = mg cos a + m v² / L avec v = w L

T = mg cos a + m w² L

au point culminant le cas limite correspond à une tension nulle soit :

mg cos a + m w² L = 0 avec a = p et cos p = -1

-g + w² L = 0 avec v = w L

-g + v² / L = 0

vitesse minimale de passage au point le plus haut : v² = g L = 9,8 *0,4 = 3,92 et v = 1,98 m/s.

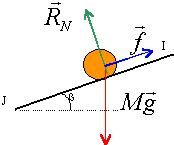
sur le plan incliné le solide est soumis à son poids, au frottement parallèle au plan et à l'action perpendiculaire au support .

projection des forces sur un axe parallèle au plan vers le bas :

a = g sin b- f / m

a= 9,8 sin 20 - 0,5 / 0,1 = -1,65 m/s² .

vitesse en J :

écrire le théorème de l'énergie cinétique entre I et J

½ mvj² - ½mv²I = mg IJ sin b - f IJ

soit v²j - v²i = 2a IJ

v²j = 4,4² + 2*(-1,65)*2 = 12,76

vj = 3,57 m/s.

durée du parcours :

la vitesse est une primitive de l'accélération :

v = a t + vi .

t = (vj-vi ) / a = (-3,57 + 4,4 ) /(-1,65 ) = 0,5 s. 

à suivre ...
retour - menu
à bientôt ...