Aurélie 01/02

trajectoire d'une balle de golf

centre étranger 97.



Google



On considére que le référentiel terrestre est galiléen et on néglige les frottements. g=9,8 m/s².

le drive :

Un golfeur se présente au départ d'un parcours de golf. Le centre d'inertie G de la balle qu'il va lancer se trouve en O. A t=0 la balle est lancée dans un plan vertical repéré par (Ox, Oy) avec une vitesse v0= 144 km/h et faisant un angle a = 40° avec l'axe Ox.

  1. Etablir les équations horaires x(t) et y(t) du mouvement de G.
    - en déduire l'équation cartésienne de la trajectoire.
    - à quelle distance du point O la balle retombe t-elle ?

approche :

La balle se trouve maintenant sur le green( terrain horizontal en O'). Le golfeur doit frapper la balle à l'aide de son club, sans la soulever pour la faire tomber dans un trou situé à 5 m de la balle.

Les forces de frottements exercées sur la balle sont supposées constantes et équivalentes à une force d'intensité f = 0,05 N. La balle se déplace en ligne droite. Le club lui communique une vitesse initiale v = 3,2 m/s (masse de la balle m=45 g).

  1. Faire un bilan des forces s'exerçant sur la balle et le représenter sur un schéma.
  2. Quelle est l'accélération de G ? En déduire la nature du mouvement de G.
  3. Etablir l'équation horaire de la position de G notée x(t).
  4. Quelle est la distance parcourue par la balle avant de s'arrêter.
    - L'approche est-elle réussie ?

 

corrigé

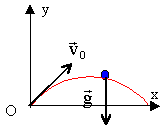
mouvement de chute libre :

accélération (0 ; -g) soit (0 ; -9,8)

vitesse initiale 144 km/h = 144/3,6 m/s = 40 m/s

v0 (40 cos a ; 40 sin a ) soit ( 30,64 ; 25,71)

position initiale, l'origine du repère.

la vitesse est une primitive de l'accélération :

vitesse à la date t : (40 cos a ; -gt +40 sin a)

la position est une primitive de la vitesse :

x = 40 cos a t (1)

y = -½ gt² +40 sin a t (2) .

(1) donne t = x / (40 cos a)

repport dans (2) : y = -½g x² / ((40 cos a)² + 40 sin a / 40 cos a) x

après simplification l'équation cartésienne de la trajectoire s'écrit :

y = -½g x² / ((40 cos a)² + tan a x

y = -0,5*9,8 / 30,64 ² x² + tan 40 x

y = -0,0052 x² + 0,839 x.

au point d'impact I sur le sol yI=0 d'où la valeur de xI.

(-0,0052 xI + 0,839 ) xI=0

xI= 0,839 / 0,0052 = 160,8 m.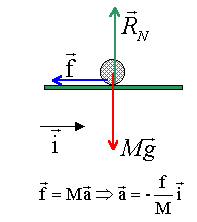

poids et action normale du plan sont opposées.

le vecteur accélération et le vecteur vitesse sont colinéaires de sens contraire :

mouvement rectiligne uniformément retardé.

vitesse initiale : v0 = 3,2 m/s

position initiale : l'origine de l'axe

vitesse : primitive de l'accélération

v = -f/M t +v0.

position : primitive de la vitesse

x(t) = -½ f/M t² + v0t.

f= 0,05 N et M= 0,045 kg d'où :

x(t) = -0,5555 t² +3,2 t

et v(t) = -1,111 t+3,2

à l'arrêt la vitesse est nulle : t = 3,2 /1,1111 = 2,88 s

distance parcourue : x= -0,5555 *2,88² +3,2 *2,88 = 4,6 m.

le trou n'est pas atteint.

à suivre ...
retour - menu
à bientôt ...