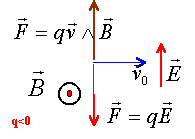|
étude d'un saut :
Un skieur de masse m = 80 kg est tiré par un bateau à l'aide
d'une corde parallèle à la surface de l'eau. Il démarre sans vitesse
initiale du point A. Le skieur lâche la corde en B et passe sur le
tremplin BC. Il arrive en C avec une vitesse Vc = 72 km.h -1
, effectue un saut, retombe sur l'eau en D.
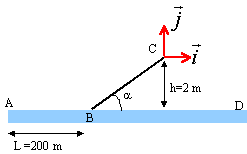
Dans tout le problème on étudiera le mouvement du centre
d'inertie G du skieur. On supposera que :
- sur le trajet AB la force de traction F de la corde est constante et
l'ensemble des forces de frottement est équivalent à une force unique f
opposée au déplacement et d'intensité f = 100 N
- de B en D tous les frottements sont négligeables. g = 10 m./s² .
- Représenter les forces qui s'exercent sur le skieur en un
point du trajet AB et en un point du trajet BC.
- Donner les expressions litterales exprimant les travaux de
ces forces s'exerçant sur le skieur au cours des trajets AB et BC .
- En utilisant le théorème de l'énergie cinétique, , exprimer
l'intensité F, tension du câble, en fonction de f , m , g , h , L, Vc )
pour que le skieur arrive en C avec la vitesse Vc.
-Calculer F
- Après le saut, donner les composantes du vecteur
accélération quand le skieur a quitté le tremplin dans le repère ( C ,
i ,j ).
- Représenter sur la figure au point C, sans échelle précise, le
vecteur vitesse du skieur lorsqu'il arrive au point C.
- Quelle est la nature de la trajectoire du skieur au cours du saut ?
Dessiner son allure sur la figure.
-Indiquer, sans justifier, la bonne expression de la vitesse Vs du
skieur au sommet S de la trajectoire parmi les expressions suivantes :
Vs = Vc ; Vs = Vc cos a ; Vs = 0.
champs électrique ou/et magnétique :
A la date t = 0 s, une particule chargée négativement pénètre
en O avec une vitesse vo dans une zone Z où règne :
- soit un champ électrique E uniforme dont la direction est
parallèle à celle du vecteur j.
- soit un champ magnétique B uniforme dont la direction est
orthogonale au plan ( O, i, j ).
Le poids de la particule sera négligé devant les autres forces
que vous prendrez en compte.
- La trajectoire de la particule dans Z, est l'arc de
parabole OS2. En argumentant votre réponse, représenter sur
la figure la force qui agit sur elle entre O et en S2 ;
précisez le sens du champ E .
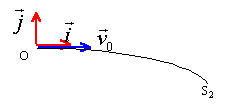
- L'énergie cinétique de la particule en S2
est-elle égale, plus grande, plus petite que celle qu'elle avait en O ?
Justifier brièvement votre réponse.
- La trajectoire de la particule dans Z est l'arc de cercle OS3.
En argumentant votre réponse ,représentez sur la figure la force qui
agit sur elle en O et en S3 ; précisez le sens du champ B.
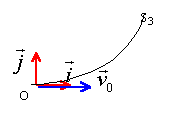
-L'énergie cinétique de la particule en S3 est elle égale,
plus grande, plus petite que celle qu'elle avait en O ? Justifier
brièvement votre réponse.
- En faisant agir les champs E et vect B simultanément, il
est possible que la trajectoire de la particule dans Z rectiligne .
Etablir la relation entre la vitesse Vo, les champs E et B pour
satisfaire à cette condition. .
corrigé
|
|
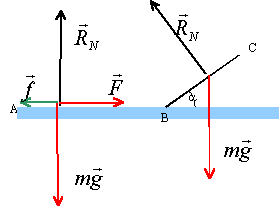
sur le parcours AB, le poids et l'action
du support, perpendiculaires au support ne travaillent pas ; seuls F et
f travaillent.
W A-->B = (F-f)L
DEc = ½ mv²B - 0 = (F-f) L
seul le poids travaille (RN
est perpendiculaire au plan) sur le parcours BC :
WB-->C = -mgh
½ mv²C -½mv²B = -
mgh
½ mv²C -(F-f) L= -mgh
(F-f) L = m(½ v²C +gh) d'où F = f + m(½ v²C +gh) / L.
vc = 72 /3,6 = 20 m/s.
F = 100 + 80 / 200 ( 0,5*20*20 + 10*2 )
= 188 N.
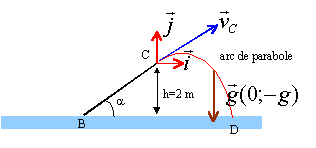
le vecteur vitesse en C est tangent au
plan incliné (20 cosa ; 20 sin a
)
la trajectoire est un arc de parabole
le mouvement est uns chute libre avec
vitesse initiale
au sommet de la parabole le vecteur
vitesse est horizontal : sa composant verticale est nulle ; sa
composante horizontale est 20 cosa .
si arc de parabole alors champ
électrique :
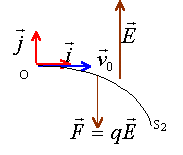
charge négative : les vecteurs champ et
force électrique sont colinéaires de sens contraire.
Entre O et S2, la composante
verticale de la vitesse augmente, alors que la composante horizontale
de la vitesse reste constante. La norme du vecteur vitesse augmente et
en conséquence l'énergie cinétique.
si arc de cercle alors champ magnétique
force centripète perpendiculaire au
vecteur vitesse ( cette force n'effectue pas de travail et ne modifie
pas l'énergie cinétique)
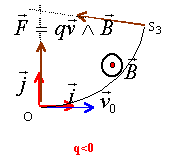
si les deux champs agissent et que la
trajectoire est rectiligne alors les deux forces électrique et
magnétique sont opposées
leurs normes sont égales : qvB = qE d'où
vB=E.
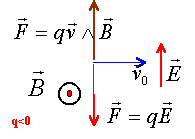
|