Aurélie déc 2001

accélération, frottement, freinage



Google



Une auto ayant une masse de 900 kg se déplace sur une route horizontale. On évalue les forces de frottement indépendantes de la vitesse à 300 N / tonne.

  1. En partant du repos, la voiture atteint une vitesse de 90 km/h en 50 secondes. Trouvez la force de traction du moteur, supposée constante et le chemin parcouru pendant le démarrage.
  2. Quelle force le moteur doit-il développer pour maintenir cette vitesse de 90 km/h ?
    - A un certain moment, le conducteur arrête le moteur sans serrer les freins. Au bout de combien de temps la voiture s'arrêtera-t-elle et quelle sera le chemin parcouru ?
  3. Lorsqu'on agit sur les freins, la voiture s'arrête après avoir parcouru 125 m, la vitesse initiale étant toujours de 90 km/h. En supposant la force de freinage constante, quelle est sa valeur ?

corrigé

frottement 300*0,9 = 270 N.

mettre la vitesse en m/s : 90 /3,6 = 25 m/s.

accélération (m/s²) = variation de la vitesse (m/s) / durée de cette variation (s) = 25 / 50 = 0,5 m/s².

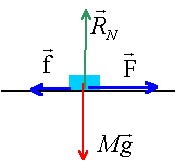
la seconde loi de Newton s'écrit sur un axe parallèle à la route ( sens du mouvement) :

-f +F = ma

F = ma + f = 900*0,5 +270 = 720 N.

distance parcourue : d = ½ a t² = 0,5 * 0,5 *50 ² = 625 m.

mouvement rectiligne uniforme donc la somme des forces est nulle (principe d'inertie)

soit -f + F= 0 d'où F = 270 N.

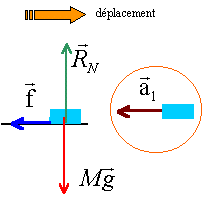
moteur à l'arrêt et freins non serrés :

la seconde loi de Newton s'écrit sur un axe parallèle à la route ( sens du mouvement) :

- f = ma1

a1 = -270 / 900 = -0,3 m/s².

utiliser la relation : v² finale - v² départ = 2 accélération fois distance

0 - v² = 2a1 d

d = 25*25 / (0,6 ) = 1041 m.

expression de la vitesse : v final = a1 tfinal + v départ.

0 = -0,3 tfinal +25

tfinal = 83,3 s.

moteur à l'arrêt et freins serrés :

à la force de frottement précédente on ajoute la force de freinage

v² finale - v² départ = 2 accélération fois distance

0 - 25² = 2a2 *125

a = -2,5 m/s².

écrire la 2 ème loi de Newton sur un axe parallèle à la route (sens du mouvement) :

-(freinage +frottement) = ma2.

ma2 = 900*(-2,5) = -2250 N

force de freinage = 2250-270= 1980 N.

retour - menu