|
. .
|
||||||
|
||||||
|
|
satellite sur une orbite circulaire : La Terre est assimilée à une sphère homogène de masse M , de centre T et de rayon R = 6380 km . On admettra que la force de gravitation ,qu'elle exerce sur les objets situés à une distance r > R de son centre T ,est la meme que si toute la masse MT était concentrée en T .On notera G la constante de gravitation et on prendra : G = 6,67 10-11 N.m2.kg-2 . Un satellite artificiel de la Terre, de masse m ,est en orbite circulaire à l'altitude h = 300 km au dessus de la Terre .
descente du satellite : Pendant cette phase, le champ de pesanteur (vecteur de ) g est
supposé uniforme (g = 10 m.s-2 ) . L'axe des z est choisi
parallèle à g et de sens opposé.Le sol terrestre supposé horizontal est
pris comme plan xOy des coordonnées . On suppose que le satellite,
freiné par un parachute, descend d'un mouvement vertical rectiligne
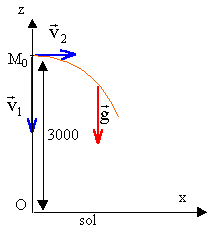
uniforme , de vitesse v1 = 10 m.s-1 . Le
satellite étant arrivé au point M0 de coordonnées (x0
= 0, y0 = 0, z0 = 3,0 km ), à un instant pris
comme origine des temps, une balise radio est éjectée horizontalement
du satellite dans le plan xOz avec le vecteur vitesse v2 (v2
= 2 m.s-1 ) par rapport au satellite : cela signifie qu'au
point M0 , la balise radio a par rapport à la Terre, le
vecteur vitesse initiale Le mouvement du satellite est supposé non modifié par l'éjection de la balise . Celle-ci tombe dans le champ de pesanteur terrestre, les frottements de l'air étant supposés négligeables .
|
|||||
|
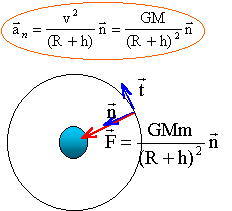
dans la base de Frenet : suivant l'axe n = GMm /(R+h)² = mv²/ (R+h) d'où la vitesse : v² =GM / (R+h) suivant l'axe t : dv/dt = 0 doù norme de la vitesse constante et mouvement uniforme. masse de la terre : mettre les distances en mètres R+h = (6380+300)103 = 6,68 106 m v² = 7,74 ² 106 = 6 107 m²/s² M= v²(R+h) / G = 6 107 *6,68
106 / 6,67 10-11 = 6
1024 kg.
le mouvement du satellite est uniforme suivant Oz : zs = -10 t +3000. durée de la chute : t= 3000/ 10 = 300 s. le mouvement de la balise est dans le plan contenant l'accélération g et le vecteur vitesse initiale. composantes du vecteur accélération : (0 ; -10) composantes du vecteur vitesse initiale : (2 ; -10) composantes du vecteur position initial : (0 ; 3000) le vecteur vitesse est une primitive du vecteur accélération : (2 ; -10t -10 ) le vecteur position est une primitive du vecteur vitesse : x = 2 t et z = -5 t² -10t +3000 équation de la trajectoire parabolique : t= 0,5 x et repport dans z z = -5 x² / 4 -10 x/2 +3000 z = -1,25 x²-5x+3000. durée de la chute : au sol z=0 soit -5t² -10t +3000 =0 t² +2t-600 = 0 résoudre et conserver la racine positive D = 4+600*4 = 2404 prendre la racine carrée de 2404 donne 49 t= (-2+49) / 2 = 23,5 s. la balise touche le sol en premier, 300-23,5 = 264,5 s avant le satellite.
|
||||||
|