Aurélie nov 2001

Mesure de la capacité d'un condensateur

Polynésie 09/00



Google



 On considère le montage suivant : R= 20 ohms; L= 0,35 H et r = 10 ohms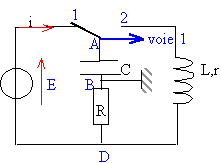

Charge du condensateur à l'aide d'un générateur de tension :

Le condensateur étant initialement déchargé, l'interrupteur est en position (1). Un dispositif ( ordinateur ou oscilloscope à mémoire ) permet d'enregistrer la tension uAB aux bornes du condensateur en fonction du temps.

  1. Expliquer le phénomène et commenter l'allure de la courbe obtenue.
  2. Déterminer, en justifiant, les valeurs de l'intensité du courant au début et à la fin de la charge.
    - Tracer l'allure de l'évolution de l'intensité en fonction du temps
  3. Déterminer à partir du graphe , en expliquant la méthode, une valeur approchée de la constante de temps du dipole (RC)
    - En déduire une valeur approchée de la capacité du condensateur.

Circuit RLC :

Le condenstateur étant chargé, l'interrupteur est basculé en position (2). On enregistre toujours la tension uAB et on obtient la courbe suivante :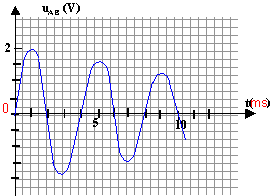

  1. Identifier le phénomène observé.*
  2. déterminer la pseudo-période de la tension.
    - La période propre de ce circuit est donnée par l'une des relations suivantes :

    Choisir la bonne relation en montrant que t est homogène à un temps.
    - En assimilant la pseudo-période à la période propre, calculer la valeur de la capacité du condensateur .
    - Si on admet un écart maximal de 10%, les deux valeurs trouvées pour C sont-elles compatibles ?

  3. Calculer l'énergie emmagasinée dans le condensateur aux dates t= 1 ms et t =5 ms.
    - Quelles sont aux mêmes instants l'énergie emmagasinnée dans la bobine et l'énergie totale du circuit ?
    - Cette dernière reste-t-elle constante ? Pourquoi ?

 

corrigé

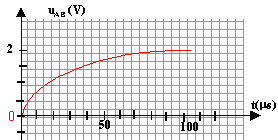
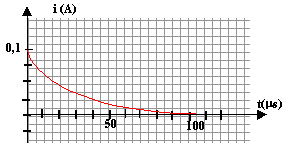
charge du condensateur :

le condensateur se charge : la tension à uAB ses bornes augmente jusqu' à atteindre la valeur 2V.

ses armatures se différentient et acquièrent des charges opposées |Q| = CuAB .

Au début de la charge la tension aux bornes du condensateur est voisine de zéro.

E = uAB + Ri donne E = R i0

La tension aux bornes du résistor R est R i0 = 2 d'où : i0 = 2 / 20 = 0,1 A

à la fin de la charge la tension uAB est égale à 2V :

E= uAB + Ri donne 2 = 2 +R ifin soit ifin=0.

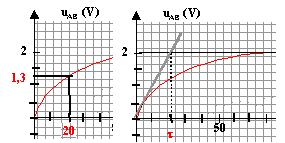
constante de temps t :

à t= t la tension uAB est égale à 0,67 fois sa valeur maxi soit 2*0,67 voisin de 1,3 V

la tangente à l'origine coupe l'asymptote à la courbe uAB à t = t.

capacité C :

20 10-6 secondes = RC = 20 C

C = 10-6 F

circuit RLC :

le condensateur chargé se décharge à travers une bobine inductive.

Il y a un échange d'énergie entre la bobine et le condensateur avec des pertes par effet joule

oscillations libres amorties.

la pseudo-période est lue sur le graphe T = 4 ms = 4 10-3 s.

la bonne relation :

inductance L homogène à : [V] [s] [A]-1.

capacité C homogène à : [C] [V]-1 soit [A] [s] [V]-1.

le produit LC est homogène à : [V] [s] [A]-1[A] [s] [V]-1 soit [s]²

racine carrée de LC homogène à un temps en seconde

d'où

élever au carré : T² = 4 p² LC

C = 16 10-6 / (4*3,14² *0,035 ) = 1,15 10-6 F.

L'écart avec la valeur précédente est de 15%.

énergie :

aux dates t= 1ms et t= 5ms, la tension aux bornes du condensateur passe par une valeur maximale:

celui-ci stocke toute l'énergie du dipole RLC

la bobine ne stocke à ces dates aucune énergie.

E= ½ CU²AB .

E= 0,5 * 10-6 * 2² = 2 10-6 J à t = 1 ms

E= 0,5*10-6 * 1,5² = 1,25 10-6 J à t = 5 ms

L'énergie totale stockée dans le dipole RLC diminue au cours du temps:

lors des échanges d'énergie entre condensateur et bobine, un courant circule dans le circuit.

la résistance du circuit est r =10 ohms; une partie de l'énergie est dissipée sous forme de chaleur (effet Joule).

à suivre ...
retour - menu
à bientôt ...