|
Asie 06/01
|
||||||
|
||||||
|
|
texte : Les vélos tout terrain sont de plus en plus souvent équipés d'une fourche à suspension . Sa présence offre confort et précision de trajectoire. La fourche comprend deux parties : La suspension : Après un choc, elle permet un retour - menu plus ou moins rapide à la position initiale. Pour cela, on dispose à l'intérieur des fourreaux, c'est à dire dans les bras de la fourche, un système équivalent à un ressort. Ce ressort transforme chaque choc dû à l'irrégularité du sol en impulsion élastique qui permet d'atténuer les inégalités du sol afin d'assurer un certain confort mais aussi un mimimum de tenue de route. Seul le système n'est pas idéal car, suite à une excitation, il peut engendrer une série importante d'oscillations dangereuses pour la tenue de route et inconfortables. Il convient donc d'adjoindre au ressort, un dispositif permettant d'amortir ses oscillations, c'est le rôle de l'amortisseur. L'amortisseur : Le plus performant reste l'élément hydraulique. On utilise l'aptitude de certaines huiles à opposer une résistance lorsqu'on les force à passer à travers un espace réduit. En agissant à la fois sur le nombre de ces passages et sur leurs tailles (clapets) , et sur la viscosité de l'huile, on arrive à régler avec précision l'importance de l'amortissement. Lors d'un choc, l'huile passe rapidement par les clapets ou les trous, offrant ainsi une résistance qui ralentit le mouvement de compression du ressort. Lorsque le ressort se détend, l'huile rejetée par les clapets qui se sont refermés, ralentit cette fois le retour - menu à la position normale, diminuant le phénomène d'oscillations. Les courbes suivantes donnent l'amplitude zm des oscillations de la suspension en fonction de la fréquence de l'excitateur pour différents réglages de l'amortissement. 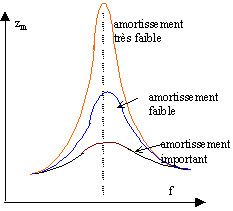 raideur du ressort : k= 10 000 N/m ; masse du vélo + cycliste : 100 mk ; g= 10 m/s². questions : étude du texte :
étude du texte : Pour l'étude de la suspension, le système sera modélisé de la façon suivante : la masse M représente la masse du vélo et du cycliste, le ressort de la fourche sera modélisé par un ressort de raideur k. On suppose que le mouvement d'oscillations s'effectue suivant un axe vertical Oz orienté vers le bas. La position du centre de gravité G par rapport à la position d'équilibre est notée z. Dans le cas où l'on tient compte de l'amortissement, l'équation différentielle régissant le mouvement du centre d'inertie s'écrit : Mz"+ lz' + kz = 0.
|
|||||
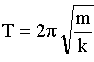
masse en kg et raideur en N/m T= 2*3,14*racine carrée ( 100 / 10 000 )= 0,628 s. amortissement faible, donc oscillations forcées peu amorties de grande amplitude. le sol joue le rôle d'excitateur. à la résonance la fréquence de l'exitateur est voisine de la fréquence propre de l'oscillateur : oscillation de grande amplitude si l'amortissement est faible (inconfort et mauvaise tenue de route) La cause de l'amortissement des oscillations est l'élément hydraulique : vixcosité de l'huile ; nombre et taille des clapets; nombre de passages à travers ces clapets. raideur : à l'équilibre le poids du vélo+ cycliste est opposé à la tension : T= mg = 100 *10 = 1000 N la tension du ressort est proportionnelle à la déformation : T= k x k= 1000 / 0,1 = 10 000 N/m. le terme lz' traduit mathématiquement l'amortissement. chaque terme de l'équation différentielle est homogène à une force soit une masse fois une accélération lz' : [kg] [m][s]-2. z' : homogène à une vitesse [m] [s]-1. l : [kg] [m][s]-2[m]-1 [s] soit : [kg][s]-1.
solution de l'équation différentielle : En absence de frottement, l'équation différentielle s'écrit : mz" + kz = 0 dérivée de la fonction cos (wt+j)--> -w sin (wt+j) dérivée de la fonction sin (wt+j)--> w cos(wt+j) z' = -zmw sin (wt+j) z" = -zmw² cos (wt+j)= -w² z repport dans l'équation différentielle : m ( -w² z) + k z est-il égal à zéro w² = k/m d'où : m ( -k/m z) + k z est bien égal à zéro. la fonction z(t) = zm cos (wt+j) est solution de l'équation différentielle. énergie mécanique : somme de l'énergie potentielle élastique et de l'énergie cinétique : ½ kz² + ½ mz'² avec z' = vitesse en l'absence de frottement l'énergie mécanique est constante : ½ kz² + ½ mz'² = constante il faut dériver cette expression par rapport au temps: dérivée de z² --> 2z z' dérivée de z'² --> 2 z' z" ½ k 2 z z' + ½ m 2 z' z" = 0 simplifier par z' : kz + mz"=0.
|
||||||
|