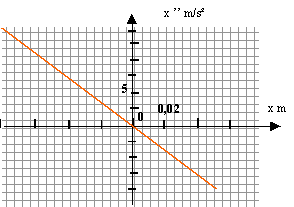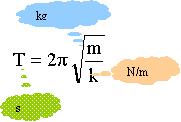Aurélie nov 2001

oscillateur mécanique horizontal

Liban 06/98



Google



 

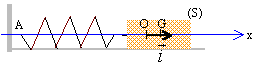
détermination de la raideur k :

Un ressort de longueur L0 à vide est accroché par une extrémité à une potence. A l'autre extrémité est suspendu un solide S de masse m. l'ensemble est vertical et la longueur du ressort devient L

  1. Etudier l'équilibre de S et exprimer k en fonction des paramètres adéquats. Calculer k si m= 100 g; L0 = 400 mm et L= 448 mm.
  2. Le ressort et S sont placés sur un banc à coussin d'air horizontal. L'extrémité libre est accrochée à un point fixe et les frottements seront considérés comme négligeables. Au repos le centre d'inertie de S est en O, pris comme origine des abscisses sur l'axe horizontal x'x. On écarte G de sa position d'équilibre et on lâche S.

    - Faire l'inventaire des forces s'exerçant sur S dans une position quelconque de G lors de son mouvement.
    - On pose OG=x : montrez que l'équation différentielle du mouvement peut s'écrire x"= - k/ m x
    - A l'aide du graphe ci-dessous déterminer la valeur de k.

    - Vérifier que la solution de l'équation différentielle précédente est de la forme : x= a sin(wt+j); en déduire l'expression de la période et la calculer.
    - Que peut-on dire des deux valeurs de k ? Par la suite on arrondira k à l'entier le plus proche.

énergie cinétique, potentielle et mécanique :

  1. Lors du mouvement précédent calculer les valeurs de la tension du ressort en A d'abscisse xA= -4 cm et en B: xB= 6 cm. Faire un schéma représentatif de ces forces en A et B.
  2. L'expression du travail de cette force de A à B est W= ½ k(xA²-xB²). Pourquoi ce travail n'est-il pas égal au produit scalaire :
    - Calculer le travail de toutes les forces appliquées à S lors du trajet AB.
  3. Enoncer le théorème de l'énergie cinétique appliqué à S lors du trajet AB.
    - La vitesse en B étant égale à 0,75 m/s, déterminer la vitesse en A.
    - rappeler l'expression littérale de l'énergie potentielle élastique du système (S + ressort ) en fonction de x et en admettant qu'elle soit nulle en x=0.
    - Déterminer l'énergie mécanique du système (S + ressort).
    - Déterminer l'amplitude du mouvement de G.

corrigé


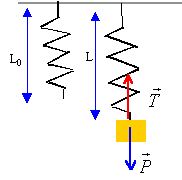
A l'équilibre tension et poids sont opposés: leurs normes sont égales

mg = k(L-L0)

masse en kg et longueur en mètre

k = 0,1*9,8 / 0,048 = 20,4 N/m.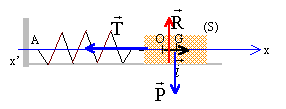

poids et action du support se neutralisent.

tension du ressort

La seconde loi de Newton s'écrit, le référentiel terrestre étant supposé galiléen :

projection sur l'axe x'x :

-k x = mx" ou x" + k/m x=0

pulsation w² = k/m

période :

calcul de T : 2*3,14 racine carrée (0,1 / 20 ) = 0,44 s.

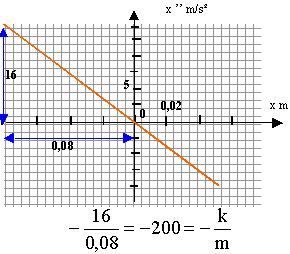
détermination graphique de k :

avec m = 0,1 kg d'où k= 200*0,1 = 20 N/m.

solution de l'équation différentielle :

x= a sin(wt+j)

dériver par rapport au temps : x' =wa cos(wt+j)

dériver une seconde fois : x'' = - w²a sin(wt+j) = - w²x

repport dans l'équation différentielle : x" + w² x=0

- w²x + w²x =0 est bien vérifiée quel que soit x.

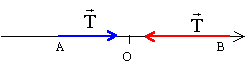
valeur de la tension :

en A : x= -0,04 m d'où T= 20*0,04 = 0,8 N

en B : x= 0,06 m d'où T = 20*0,06 = 1,2 N.

travail de forces :

Poids et action du support sont perpendiculaires au support : ces forces ne travaillent pas.

La tension n'est pas une force constante, le travail de la tension ne peut pas être calculée à partir du produit scalaire.

travail de la tension : W(T) = 0,5*20 ( 0,04²-0,06²)= -0,02 J.

la variation d'énergie cinétique entre deux dates t1 et t2 est égale à la somme des travaux des forces agissant sur le système entre ces deux dates

½ mv²B -½ mv²A = W(T) = -0,02

v²A = v²B +0,02*2 / m = 0,75² +0,02*2 / 0,1 = 0,9625.

vitesse en A : 0,98 m/s.

énergies :

énergie potentielle élastique : ½ k x²

énergie mécanique :

au départ : ½ ka² ( entierement sous forme potentielle élastique)

à la date t : ½ kx² + ½mv²

au passage à la position d'équilibre : ½ mv² max ( entierement sous forme cinétique )

en A : E = 0,5 *20 *0,04² + 0,5 * 0,1 *0,98² = 0,064 J

0,5 *10*a² = 0,064

a² = 0,0128 d'où l'amplitude a = 0,113 m.

à suivre ...
retour - menu
à bientôt ...