Aurélie oct 2001

étude d'un pendule

Nlle Calédonie 12/00



Google



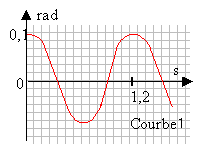
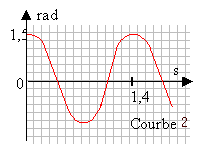
dispositif :

On étudie les oscillations d'un pendule. L'objectif est de chercher dans quelles conditions ce pendule peut être assimilé à un oscillateur harmonique. Le pendule est constitué d'uncorps de petites dimensions, de masse m, suspandu à un fil de longueur L. Le pendule est écarté d'un angle a0 de sa position d'équilibre et laché sans vitesse initiale.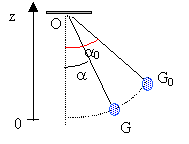

Étude expérimentale :

Un dispositif approprié a permis d'enregister les courbes 1 et 2.

  1. Déterminer graphiquement dans chaque cas la période et la valeur de l'angle a0.
  2. La modélisation de cependule par un oscillateur harmonique donne T=1,13 s pour la valeur de la période, quel que soit la valeur de a0 (dans les limites d'un certain intervalle). En déduire si le pendule étudié se comporte, dans chacun des cas étudié, come un oscillateur harmonique.

Étude théorique :

  1. Représenter sur un schéma les forces s'erxerçant sur la petite boule fixée au fil.
  2. Exprimer le travail de chaque force au cours d'un déplacement G0G en fonction de m, L, g, a et a0.
  3. En appliquant le théorème de l'énergie cinétique montrer que : a'²=2g/L (cosa-cosa0).
    On donne la vitesse de G à la date t : v = La' avec a' = da /dt
  4. En dérivant l'expresion obtenue à la question précédente, montrer que l'équation différentielle du pendule est :
    a'' + g/L sina=0
    On rappelle que d(cosa )/dt = -sina et que d(a' ²) /dt = 2a' a" .
  5. L'équation différentielle de l'oscillateur harmonique est : a' '+g/L a =0
    - Quelle approximation doit-on faire pour assimiler le pendule expérimental à un oscillateur harmonique ?
    - Compare les valeurs de a0 en radian et sina0 pour les deux expériences précédentes. Dans quelle expérience le pendule peut-il être assimilé, de façon satisfaisante, à un oscillateur harmonique ? Justifier.

 

corrigé


lectures graphes :

les périodes sont T1=1,2 s et T2 = 1,4 s

les amplitudes angulaires a0 sont 0,1 rad et 1,5 rad.

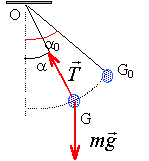
la petite boule est soumise à deux forces: son poids et la tension du fil

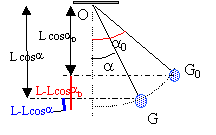
travail des forces :

La tension est toujours perpendiculaire à la vitesse : cette force ne travaille pas.

le travail du poids est égal à : mg ( zG-zG0)

l'origine des altitudes est prise au point le plus bas, la position d'équilibre.

mg ( zG0 -zG) = mg ( L-Lcosa0 -L+Lcosa)

mg ( zG-zG0) = mgL(cosa -cosa0 ).

La variation de l'énergie cinétique est égal au travail des forces agissant pendant la durée de cette variation.

l'énergie cinétique initiale est nulle.

½ mv²fin - 0 = mgL(cosa -cosa0 )

v²fin = 2 gL(cosa -cosa0 )

v= La' d'où : L² a'² = 2 gL(cosa -cosa0 )

diviser chaque membre par L² :

a'² = 2 g /L(cosa -cosa0 ).

équation différentielle :

On dérive par rapport au temps l'expression précédente :

2a'a" = 2g / L (-sina) a '

diviser chaque membre par 2a' :

a" = g / L (-sina)

a" +g / L sina=0.

approximation : si l'angle est petit, on peut assimiler le sinus de l'angle et la mesure de l'angle en radian.

a" +g / L a=0.

si a0 = 0,1 rad alors sin a0 = 0,0998

sin 0,1 voisin de 0,1 rad; l'approximation est possible et le pendule dans ce cas se comporte comme un oscillateur harmonique

si a0 = 1,5 rad alors sin a0 = 0,997

sin 1,5 est différent de 0,997 rad; l'approximation n'est pas possible et le pendule dans ce cas ne se comporte pas comme un oscillateur harmonique.

à suivre ...
retour - menu
à bientôt ...