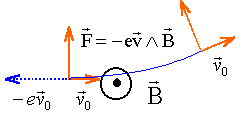|
bac
Nlle calédonie 12/00
|
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
extrait d'un livre : En 1897 le physicien anglais J Thomson découvrit l'électron en étudiant la nature des rayons cathodiques produits lors de décharges électriques dans un gaz raréfié. Il chercha à déterminer la nature des particules chargées négativement constituant les rayons cathodiques en les soumettant successivement à des forces électriques et à des forces magnétiques. Le faisceau de particules arivent avec une vitesse v0 horizontale dans une région de déviation R1 de longueur l =5 cm dans laquelle il est soumis soit à une force électrique soit à une force magnétique. Puis le faisceau se propage en ligne droite dans la région de propagation R2 de longueur L=1,1 m dans laquelle n'existe ni champ électrique ni champ magnétique. Il atteint l'écran à l'extrémité du tube où il crée une tache lumineuse dont J Thomson mesurait la déviation d par rapport à la direction de v0. En utilisant la deuxième loi de Newton, J Thomson avait établit la relation approchée d = F l L / (mv0²) (1), où m représente la masse de la particule et F la valeur de la force électrique ou magnétique dans la région R1. Connaissant la valeur E du champ électrique ou B du champ magnétique crées dans R1 ainsi que les valeurs des déviations correspondantes delec et d mag J Thomson calculait v0 puis le rapport m / |q| où q représente la charge électrique d'une particule. tableau des résultats :
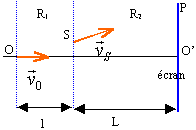 Questions: Les particules sont des électrons et on ne tient pas compte de leur poids. déviation dans un champ électrique uniforme : les électrons pénètrent en O avec une vitesse v0 dans la région R1 où ils sont soumis à un champ électrique uniforme tel que le vecteur champ E soit perpendiculaire à la vitesse v0. Ce champ est dans le plan de la figure. Ils sortent en S avec une vitesse vS.
déviation dans un champ magnétique uniforme : On considère le même dispositif mais dans R1 règne un champ magnétique uniforme B, perpendiculaire au plan de la figure.
mouvement des électrons dans R2: Au dela de S les électrons sont en mouvement dans la région R2. Ils arrivent sur l'écran au point P en ayant subi une déviation d =O'P. A l'aide des hypothéses de l'énoncé, justifier par une démonstration l'expression " région de propagation rectiligne".
|
|||||||||||||||||||||||||||||||||||||
|
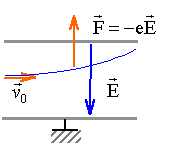
les électrons sont déviés du coté de S (vers le haut) . La force électrique est verticale vers le haut, en O comme en S, le champ électrique restant vertical. le champ électrique est colinéaire à la force électrique. Ces deux vecteurs sont de sens contraire, la charge des électrons étant égal à -e (charge élémentaire) le champ électrique est dirigé vers le plus petit potentiel. La trajectoire des électrons est un arc de parabole.
champ magnétique : Les électrons sont soumis à la force de Lorentz, centripète, dirigée vers le centre de l'arc de cercle.
la force de Lorentz est à chaque instant perpendiculaire à la vitesse : en conséquence la puissance de cette force est nulle; la norme de la vitesse ne change pas ( la direction de la vitesse change): le mouvement est uniforme.
région R2 : le poids des électrons étant négligeable, les électrons ne sont soumis à aucune force dans la région R2. d'après le principe d'inertie, le mouvement de ces derniers est rectiligne uniforme valeur de la force électrique : F= |q| E = eE delec = eE l L/ (mv0²) valeur de la force magnétique : F= |q|v0B = ev0B dmag = eB l L/ (mv0) delec /dmag = E/ (Bv0) d'où v0= E dmag / (Bdelec ) dans la dernière ligne du tableau, les déviations étant les mêmes : v0= E / B = 1,5 104 / 5,5 10-4 = 2,7 107 m/s. l'une ou l'autre expression des déviations permettent de calculer le rapport m / e : les longueurs s'expriment en mètre. m/ e = B l L / (v0 dmag) =5,5 10-4 *0,05*1,1 / ( 2,7 107 *0,08) = 1,4 10-11 kg /C.
|
||||||||||||||||||||||||||||||||||||||
|