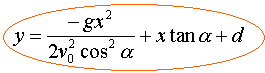Aurélie oct 2001

Frédéric et son pistolet

bac Polynésie 09/00



Google



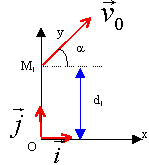
Frédéric décide d'utiliser ces connaissances en mécanique pour étudier le mouvement de la flèche tirée par son pistolet. Négligeant l'action de l'air et prenant g=10 m/s², il considère la fléche comme un objet ponctuel de masse m= 50g et de vitesse initiale v0. La flèche est tirée d'un point M, à la distance d au dessus du sol, avec une vitesse v0 inclinée d'un angle a sur l'horizontale.

Etude théorique du mouvement de la flèche:

  1. Etablir sous forme littérale les équations horaires du mouvement de la flèche après son lancement. L'instant initial est celui où la flèche se trouve au point M.
  2. En déduire l'équation de la trajectoire et sa nature.
  3. Johann se trouve sur le sol horizontal à 15 m devant le point O: risque t-il de recevoir la flèche si celle ci est tirée depuis le point M1 (d1 = 1,5 m) avec une vitesse initiale v0 =10 m/s et a=40° ?

 

détermination expérimentale de v0 :

  1. tir vertical : le pistolet est en M2 tel que d2 = 1,7 m. La fléche retombe sur le sol 2,2 s après son départ. Calculer la valeur de la vitesse initiale en utilisant les équations précédentes.
  2. tir horizontal :
    Le pistolet est maintenu horizontal en M3 tel que d3 = 1,2 m. La flèche touche le sol en un point B qui appartient au même plan que O, à une distance de O égale à 4,9 m. Calculer la valeur de la vitesse initiale en utilisant les équations précédentes.
  3. étude énergétique du système ressort-flèche :
    - Le ressort qui se trouve à l'intérieur du pistolet est horizontal, de masse négligeable devant la masse de la flèche, de constante de raideur k =220 N/m. Sa longueur à vide est l0=20 cm et sa longueur minimale est lm=5 cm. l'énergie potentielle élastique d'un ressort est Ep= ½k    Dl² , Dl est la variation de longueur du ressort. Donner l'expression de l'énergie mécanique de ce système en fonction de Dl, de la vitesse de la flèche (tant qu'elle reste en contact avec le ressort) .
    - En déduire la valeur de la vitesse     v0 de la flèche lorsqu'elle se sépare du ressort.

 

corrigé


équations horaires :

système : la flèche; référentiel terrestre galiléen.

Ecrire la seconde loi de Newton, la fléche étant soumise uniquement à son poids.

d'où l'accélération :

vitesse initiale :

le vecteur vitesse est une primitive de l'accélération :

vx = v0 cosa et vy = -gt + v0 sina.

position initiale x0 = 0 et y0 = d

le vecteur position est une primitive du vecteur vitesse :

x= v0 cosa t

y = -½gt² + v0 sina t +d

éliminer le temps entre ces deux relations pour trouver la trajectoire:

t = x / (v0 cosa )

repport dans y :

la trajectoire est un arc de parabole.

cos²40 = 0,587 ; v0² = 100 ; tan 40 = 0,839

y = -0,0851 x²+ 0,839 x +1,5

lorsque la flèche touche le sol y=0

-0,0851 x²+ 0,839 x +1,5 =0

ou bien en divisant chaque membre par -0,0851 :

x²-9,85 x -17,62 =0

résoudre : D=167,48

x1= ½(9,85+12,94)= 11,4 m.

Johann n'est pas atteint

tir vertical : l'angle a vaut 90°

les deux équations horaires ci-dessus s'écrivent : x=0 et y = -½gt² + v0t +d

y= -5t² + v0t +1,7

à t= 2,2 s, la flèche est sur le sol y=0

0= -5*2,2² + 2,2v0 +1,7 d'où v0 = 10,2m/s.

tir horizontal : l'angle a vaut 0°

les deux équations horaires ci-dessus s'écrivent : x = v0 t et y = -5 t² + 1,2

trajectoire : y = -5x² / v0² +1,2

la fléche touche le sol : y = 0 ; x= 4,9 m

v0² = 5*4,9² / 1,2 = 100 et v0 = 10m/s.

aspect énergétique :

ressort comprimé au maximum:

l'énergie du système ressort flèche vaut : 0,5*220* 0,15² =2,475 J

ressort comprimé et flèche en contact, l'énergie est en partie sous forme potentielle élastique et en partie sous forme cinétique

½ k Dl² + ½ mv²

la fléche se sépare du ressort lorsque Dl =0; l'énergie su système est sous forme cinétique ½mv0²

l'énergie mécanique de ce système se conserve :

2,475 = ½mv0²

v0² = 2,475 *2 / 0,05 = 99

v0 = 9,95 m/s.

à suivre ...
retour - menu
à bientôt ...