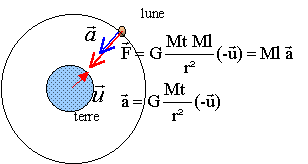
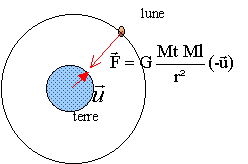
On admet que la terre et la lune ont une répartition de masse à symétrie sphérique et que la lune se déplace sur une orbite circulaire autour de la terre. On appelle r la distance entre les centres des deux astres.

1. Faire le schéma de l'orbite de la lune dans le référentiel géocentrique et représenter la force gravitationnelle exercée par la terre.
2. La valeur du champ de gravitation terrestre est donnée par la relation g=GM / r².
   - préciser ce que représente chaque lettre.
   - Etablir l'expression de g en fonction de g₀ (valeur du champ de gravitation au nveau du sol), R rayon terrestre et r.
3. Mouvement de la lune :
   - Appliquer la 2 ème loi de Newton à la lunedans le référentiel géocentrique suposé galiléen. Exprimer le vecteur accélération du centre d'inertie de la lune.
   - Soit V la vitesse de la lune sur son orbite. Donner les caractéristiques du vecteur accélération du centre de la lune en mouvement circulaire uniforme.
   - Montrer que l'expression de g₀ est donnée par : g₀ = V² r /R².
4. Depuis l'antiquité on sait que r=60 R et que la période de révolution de la lune est T=27 jours 7 heures 43 minutes. En 1670 Jean Picard par une méthode de triangulation trouve une valeur de R de 6370 km. En 1686 Isac Newton utilise ces données pour déterminer la valeur de g₀. Exprimer V en fonction de T et de r; retrouver la valeur de g₀ déterminée par Newton.
5. En 1796 Henry Cavendish mesure G à l'aide d'une balance de torsion. Il obtient G=6,670 10^-11 N m² kg^-2; g₀ étant connu, on peut alors déterminer la masse de la terre.
   -Déterminer lamassede la terre avec les données suivantes : g₀ =9,81 ms^-2 et R= 6370 km.
6. En l'an 2000 deux physiciens de l'université de Washington améliorent le dispositif de Cavendish et obtiennent une valeur de G comprise entre 6,674 1 10^-11 et 6,674 4 10^-11N m² kg^-2;
   - pour les physiciens d'aujourd'hui la terre est-elle plus légère ou plus lourde que pour Cavendish?