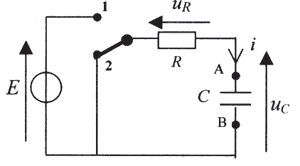
Le montage ci-contre permet d'étudier l'évolution de la tension uc aux bornes d'un condensateur de capacité C en série avec une résistance R. Le commutateur (interrupteur à plusieurs positions) a deux positions possibles repérées par 1 et 2. Une interface, reliée à un ordinateur, permet de saisir les valeurs instantanées de cette tension u_c. Initialement, le commutateur est depuis longtemps en position 2 et le condensateur est déchargé. Donnée : E = 5,0 V

1. Dès lors, comment faut-il manipuler le commutateur pour obtenir la courbe ci-dessous donnant l'évolution de la tension uc aux bornes du condensateur en fonction du temps ?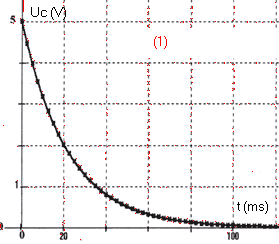

 

2. En respectant les conventions d'orientations du schéma du circuit :

• préciser le signe de l'intensité i du courant lors de la décharge ;
• écrire la relation entre l'intensité i du courant et la tension u_R ;
• écrire la relation entre la charge q de l'armature A du condensateur et la tension u_C ;
• écrire la relation entre l'intensité i et la charge q ;
• écrire la relation entre les tensions u_R et u_C lors de la décharge.
• En déduire que, lors de la décharge, l'équation différentielle vérifiée par la tension u_C est de la forme :

• Identifier le rapport . 1/ a
• Ce rapport est appelé constante de temps du dipôle RC. En recherchant son unité, justifier cette appellation.

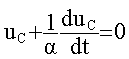
3. La solution de l'équation différentielle précédemment établie est de la forme : u_C=E exp (-at). La tension u_C est exprimée en volts. Etablir l'expression du logarithme népérien de sa valeur, notée ln u_C. On rappelle que ln ab = ln a + ln b ; ln ax = x. ln a ; ln e = 1.

• On a tracé, à l'aide d'un logiciel, la courbe représentant ln u_C en fonction du temps

• Montrer que l'allure de cette courbe est en accord avec l'expression obtenue.
• Avec laquelle des trois valeurs proposées pour la constante de temps , les résultats de la modélisation vous semblent-ils en accord ? 0,46 ms ; 2,2 ms ; 22 ms

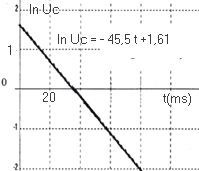
4. Le logiciel permet de créer deux nouvelles grandeurs : p=100Uc/E et n = at

p = 100 représentant le pourcentage de charge restant à la date t

n = = représentant la durée de la décharge en unités de constante de temps (c'est à dire quant t = t , n = 1; t = 2t, n = 2, etc ...).

La courbe ci-dessous représente p en fonction de n.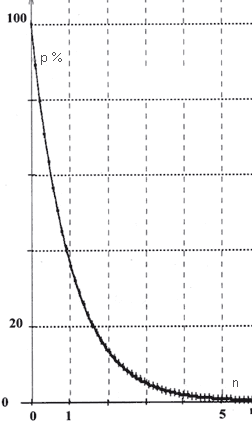

Pour n = 1, déterminer graphiquement le pourcentage de charge restante.

. Pour quelle valeur de n, la décharge peut-elle être considérée comme terminée ?

Quelle est la durée minimale pendant laquelle le commutateur doit rester dans la position convenable pour que la charge du condensateur puisse être considérée comme totale ?