| |
oscillations électriques forcées d'un circuit RLC Pondichéry 05/01 sans calculatrice
|
||||||
|
|||||||
|
|
schéma, fréquence propre bande passante |
Résonance d'intensité. On se propose d'étudier la résonance d'intensité d'un circuit série comportant une bobine, une boîte de résistances, un condensateur et un générateur de signaux basses fréquence (G.B.F.). Liste du matériel utilisé Un GBF qui délivre une tension alternative sinusoïdale de fréquence f réglable, dont la valeur est affichée sur l'écran digital de l'appareil. Une bobine d'inductance L et de résistance r = 10 W. Une boîte de résistances réglée sur la valeur R = 10 W. Un condensateur de capacité C = 1 µF. Un oscilloscope bicourbe. Un ordinateur équipé pour mesurer en mode multimètre l'intensité efficace I dans le circuit et la tension efficace U aux bornes du GBF. 1ère partie : Recherche de la résonance. le dipôle constitué de la bobine, la boîte de résistances et le condensateur montés en série est alimenté par le GBF. En utilisant l'oscilloscope, on veut visualiser simultanément la tension u(t) aux bornes du GBF sur le voie A et une tension proportionnelle à l'intensité i(t) du courant qui traverse le circuit sur la voie B. 1 - Dessiner le schéma du montage à réaliser en faisant apparaître les branchements de l'oscilloscope. 2 - On règle la fréquence du signal délivré par le GBF pour observer sur l'écran de l'oscilloscope deux courbes en phase ce qui caractérise la résonance d'intensité. La valeur de la fréquence fR correspondante est voisine de 500 Hz. a) Que représente cette fréquence fR pour le dipôle ? b) Quelle est la relation entre cette fréquence fR et les caractéristiques du dipôle ? En déduire une valeur approchée de l'inductance L de la bobine (on prendra p² =10). 2 ème partie : Courbe de réponse en intensité du circuit Grâce à l'ordinateur on mesure l'intensité efficace I dans le circuit précédent et la tension efficace U aux bornes du GBF pour différentes valeurs de la fréquence f de la tension sinusoïdale délivrée par le GBF. Le logiciel utilisé permet alors de représenter les variations de I en fonction de f tout en vérifiant que la valeur efficace U de la tension fournie par le GBF reste constante et égale à 2,0 V. La courbe obtenue est fournie dans l'annexe (page 8) à rendre avec la copie. (courbe ci dessous) 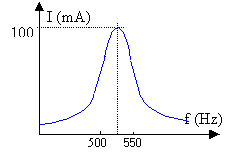
3 Déterminer graphiquement la valeur de la fréquence fR. 4 Définir la bande passante à 3 dB, la faire apparaître sur la courbe et donner sa largeur b (on prendra 1/ racine carrée (2)=0,707). 5 Le facteur de qualité étant défini par Q = fR / b , en donner une valeur approchée. 6 A partir de la courbe, déterminer, en la justifiant, la valeur de la résistance totale RT du circuit. Celle-ci est-elle en accord avec données fournies dans l'énoncé ? 7 - On montre que Q est aussi donné par la relation où RT est la résistance totale du dipôle. Calculer une valeur approchée de Q. Est-elle en accord avec celle déterminée à la question 5 ? 8 - On modifie le réglage de la boîte de résistances en augmentant la valeur de R : préciser pour les grandeurs ci-dessous si elle est modifiée et, si oui, dans quel sens a) la fréquence de résonance fR ; b) la largeur b de la bande passante, c) le facteur de qualité Q
|
|||||
| |

à la résonance la fréquence du GBF est égale à la fréquence propre du dipole RLC. fp=1 / (2p racine carrée (LC)) L = 1 / (500² *4 p²* 10-6 ) = 1/ 10 = 0,1 H.
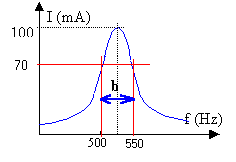
fréquence propre ( fréquence de résonance)= 520 Hz bande passante voisine de 50 Hz. ( ensemble des fréquences telles qu l'intensité du courant soit supérieure à la valeur maxi (100 mA) divisée par racine carrée de 2) facteur de qualité : 520 /50 voisin de 11. A la résonance l'impédance du circuit RLC est minimale , égale à la résistance totale du dipole RLC . L'impédance est égale à la tension efficace aux bornes du dipole divisée par l'intensité efficace (lue sur le graphe 0,1A). Z=2/0,1 = 20 ohms, ce qui correspond bien à la somme r+R = 10+10. Q= 1/20 racine carrée (0,1 / 10-6 ) = 0,05 racine carrée(105) = 0,05*100 racine carrée (10) voisin de 15 , du même ordre de grandeur que la valeur calculée précédemment. Lorsque la résistance augmente la résonance devient floue : le pic est moins aigû. La fréquence de résonance est très peu modifiée, la bande passante est plus grande et en conséquence le facteur de qualité est plus petit.
|
||||||
| |
|
||||||