Aurélie mai 2001


devoirs en terminale S

mouvement d'une balle de tennis Japon 06/97

 


Google



1

 

 

énergie, caractéristiques d'un tir

On étudie le mouvement d'une balle de tennis considérée comme un point matériel. Le mouvement est filmé à l'aide d'un caméscope dont l'axe de visée est perpendiculaire au plan de la trajectoire. La première image est prise à la date t=0 et on considère qu'à cette date les coordonnées x et z sont nulles.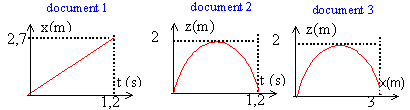

 

  1. Parmi ces courbes, laquelle représente la trajectoire de la balle. Justifier
  2. D'après le document 1, quelle est la nature du mouvement de la projection de la balle sur Ox. Calculer la composante vx du vecteur vitesse.
  3. Calculer la composante vz du vecteur vitesse à la date t=0 en précisant le graphe utilisé.
  4. Calculer la valeur a de l'angle de tir à t=0.
  5. Les documents 5,6 et 7 représentent les énergies mécaniques, cinétiques et potentielle. Identifier chaque graphe en justifiant la réponse sans faire de calculs.
  6. Déterminer la date et la position de la balle pour laquelle l'énergie cinétique du système est minimale. A cette date, quelle est la valeur de chaque composante du vecteur vitesse?

corrigé


 

Le document 3 représente la trajectoire de la balle : altitude z(t) en fonction de l'abscisse x(t) alors que les documents 1 et 2 représentent les équations horaires altitudes et abscisses en fonction du temps.

Document 1 : la fonction x(t) est une fonction linéaire : la composante de la vitesse vx suivant l'axe des x est constante. La valeur de vx est égale au coefficeint directeur de la droite soit :

2,7 /1,2 = 2,25 m/s.

Le mouvement de la balle projeté sur Ox est rectiligne uniforme.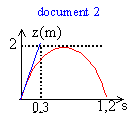

 

le vecteur vitesse est la dérivée du vecteur position par rapport au temps

tracer la tangente à la parabole à t=0 puis chercher son coefficient directeur

vz voisine de 2/0,3 = 6,66 m/s

ou bien document 4 prendre l'ordonnée à l'origine

calcul de l'angle de tir : tan a = vz / vx à t=0.

tan a = 6,66 / 2,25 = 2,96 d'où a = 71°.

aspect énergétique :

document 5 : l'origine de l' énergie potentielle de pesanteur est prise au sol.

l'énergie potentielle de pesanteur est nulle à t=0, puis croît. L'altitude maxi étant atteinte, l'énergie potentielle de pesanteur décroît jusqu' zéro.

document 7 : l'énergie cinétique proportionnelle au carré de la vitesse est maximale à t=0, puis décroît jusqu'à ce que l'altitude maxi soit atteinte. L'énergie cinétique passe par une valeur minimale ½ mv²x, puis croît ensuite lors de la descente de la balle.

document 6 : l' énergie mécanique de la balle se conserve (seul le poids travaille, les frottements sur les couches d'air sont négligés). Le graphe document 7 est voivin d'une droite horizontale dont l'ordonnée est voisine de 3,5 J

L'énergie mécanique est la somme des énergies cinétique et potentielle de pesanteur.

L'énergie cinétique est minimale, égale à ½ mv²x ; la composante verticale vz de la vitesse est nulle lorsque l'altitude maxi est atteinte. A cette altitude l'énergie potentielle de pesanteur est maximale.

date de passage à cette altitude maxi : 0,6 seconde en tenant compte de la symétrie de la parabole.


à suivre ...
retour - menu
à bientôt ...