Aurélie 01/02

optique

oculaire, microscope , réseau , niveau d'énergie physique de laboratoire 98


Google



partie A : étude d'un microscope

 

  1. L'oculaire de symbole (4, 3, 2) est constitué de 2 lentilles minces L1 et L2 . On désigne respectivement par O1 et O2 leurs centres optiques et par f '1 et f '2 leurs distances focales. La distance séparant les centres optiques est mes algébrique O1O2.
    - Ecrire la relation qui lie f '1, e, et f '2 au symbole (4, 3, 2) du doublet. On désignera par "a" la valeur commune des rapports.
    - Si mes. algébrique O1O2 vaut 45 mm, calculer f '1, f '2 et la distance focale f ' = mesure algébrique H'F' de l'oculaire. Montrer que la puissance de l'oculaire est 25     d.
    - Déterminer par le calcul les positions de F et F', H et H'.
    -Vérifier ces résultats par une construction graphique.
    - Le doublet est-il positif ou négatif ? convergent ou divergent ?
    - La relation d'achromatisme est-elle vérifiée ?
  2. L'objectif est un système convergent de foyers F et F ' et de distance focale image j ', il donne d'un objet AB une image A1B1 telle que mes.algébrique F 'A1 = 18 cm. Sachant que le grandissement de l'objectif est tel que : g = - 60, calculer sa distance focale j ' ; en déduire la distance foyer objet - objet, mes.algébrique FA.
  3. L'objectif et l'oculaire sont associés pour réaliser un microscope ; il est utilisé par un observateur à vue normale dont la distance minimale de vision distincte est 25 cm.
    - Calculer la puissance du microscope et son grossissement commercial.
    - L'intervalle optique     D vaut 18 cm. L'oeil placé au foyer F' de l'oculaire, observe l'image définitive A'B' à l'infini. Où se trouve l'image intermédiaire A1B1 ? En déduire, la distance objet mes.algébrique FAR.
    - L'oeil, toujours placé au foyer F' de l'oculaire, voit l'image définitive à 25 cm ( mes. algébrique F'A' =-0,25 m). Calculer les mesures algébriques FA1,     F 'A1 , puis la distance objet mes.algébrique FAP.
    - En déduire la latitude de mise au point du microscope.

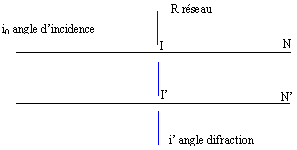
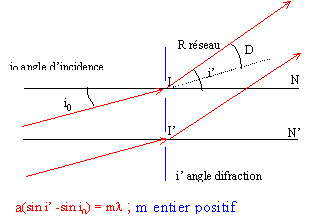
partie B : étude d'un réseau

Dans toute cette partie, le réseau est éclairé par une lampe à sodium assimilée à une source monochromatique de longueur d'onde l = 589,3 nm (valeur moyenne du doublet du sodium).

  1. Ecrire la relation fondamentale des réseaux (par transmission).
    Pour cela, on appellera i0 l'angle d'incidence et i' l'angle de diffraction. Reproduire sur la copie le schéma représentant le réseau ; le compléter en faisant apparaître les rayons incidents et diffractés ainsi que la convention de signe adoptée.
  2. La déviation D varie en fonction de l'angle de diffraction i' et passe par un minimum Dm. On admettra que le minimum de déviation correspond aux deux cas possibles i' = i0 et i' = -i0. Démontrer qu'au minimum de déviation on a :
    2a sin (Dm/2) = kl.

    Dans cette formule : a désigne le pas du réseau ; l désigne la longueur d'onde de la source monochromatique utilisée ; k désigne l'ordre du rayon diffracté.
    - On trouve Dm = 20,41° pour l'ordre 2. Calculer le pas du réseau et le nombre de traits par millimètre.

  3. Le réseau est maintenant orthogonal au faisceau incident issu du collimateur. Quel est le nombre d'images de la fente que l'on pourrait théoriquement observer derrière le réseau ?
    - La source précédente éclairant le collimateur est remplacée par une source polychromatique dont les longueurs d'ondes sont comprises entre 400 nm et 780 nm. Y a-t-il risque de chevauchement du spectre d'ordre 2 avec les ordres voisins ?

corrigé


f '1 / 4 = e / 3 = f '2 / 2 = a

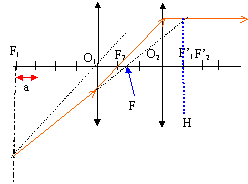
si e = 0,045 m alors a = 0,015

f '1 = 0,015 * 4 = 0,06 m et f '2 = 0,015 * 2 = 0,03 m.

distance focale f ' de l'oculaire :

1/ f ' = 1/ f '1 + 1 / f '2 -e / (f '1 f '2)

1/ f ' = 1 / 0,06 + 1 / 0,03 - 0,045 / (0,06*0,03)

1/ f ' = 50-25= 25 et f ' = 1/25 = 0,04 m.

la puissance de l'oculaire est 1/f ' = 1/ 0,04 = 25 dioptries.

cet oculaire est convergent, la distance focale image, mesure algébrique H'F ' est positive.

mes. algébrique FO1 = 4(2-3)*0,015 / 3 = -0,02 m donc oculaire négatif.

plans principaux :

mes. algébrique O2H ' = -3*2 *0,015/ ( 4+2-3) = -0,09 / 3 = -0,03 m.

mes. algébrique O1H = 3*4 *0,015/ ( 4+2-3) =0,18 / 3 = 0,06 m.

la relation d'achromatisme e =½( f '1+ f '2) = 0,5 ( 003+0,06) =0,045 m est vérifiée.
l'intersection entre un rayon incident parallèle à l'axe optique principal et le rayon émergent donne H'.

Le rayon émergent coupe l'axe optique principal en F '
l'intersection entre un rayon émergent parallèle à l'axe optique principal et le rayon incident donne H.

Le prolongement du rayon incident coupe l'axe optique principal en F
le marquage d'un oculaire comporte, comme celui des loupes, le grossissement.

formule de Newton appliquée à l'objectif :

j ' = -0,18 / -60 = 0,017 m

mes. algébrique FA = -0,017² / 0,18 =1,6055 10-3 m.

puissance et grossissement du microscope :

grossissemnt de l'oculaire = 0,25 / H'F' = 0,25 / 0,04 = 6,25

valeur absolue du grandissement de l'objectif : 60

grossissement commercial du microscope : 6,25* 60 = 375.

puissance intrinsèque : 4*375 = 1500 dioptries.

latitude de mise au point :

observation de l'image définitive à l'infini, alors l'image intermédiaire A1B1 se trouve dans le plan focal objet de l'oculaire.

mes.algébrique F' A1 = -D = -0,18 m

on utilise la formule de Newton (ci-dessus) appliquée à l'objectif, pour trouver mes. algébrique F AR sachant que mes. algébrique F' A1 = 0,18 m et que j ' = 0,04 m

mes. algébrique F AR = - 0,017 ² / 0,18 = -1,605 10-3 m

image définitive à la distance minimale de vision distincte :

on utilise la formule de Newton (ci-dessus) appliquée à l'oculaire, pour trouver mes. algébrique FA1 sachant que mes. algébrique F'A' = -0,25 m et que f ' = 0,04 m

mes. algébrique FA1 = - 0,04 ² / (-0,25) =6,4 10-3 m

mes . algébrique F 'A1 = mes . algébrique F 'F + mes . algébrique FA1 = 0,18 + 6,4 10-3= 0,1864 m.

on utilise la formule de Newton (ci-dessus) appliquée à l'objectif, pour trouver mes. algébrique F AP sachant que mes. algébrique F' A1 = 0,1864 m et que j ' = 0,017 m

mes. algébrique F AP = - 0,017 ² / 0,1864 = -1,550 10-3 m

latitude de mise au point : 1,605 10-3 -1,550 10-3 = 5,5 10-5 m.

réseau :

la déviation est minimale pour i' = -i0.

or la déviation est i'-i0 donc Dm = -2 i0.

par suite : a( sin (-i0 )- sin i0) = 2a sin (-i0) =2a sin (½Dm) = m l.

si ½Dm =0,5* 20,41 = 10,205° ; m = 2 ; l=589,3 10-9 m alors :

a = 2*589,3 10-9 / (2 sin 10,205) = 3,326 10-6 m.

nombre de traits par mètre : 1/a = 3 105 soit 300 traits / mm.

le nombre de maxima principaux est fini :

pour i0 =0 ; a = 3,326 10-6 m ; l=589,3 10-9 m

a sin i' = kl. soit sin i' = kl/a = k* 589,3 10-9 / 3,326 10-6 = 0,177 k

k =1 donne i1' = + ou - 10,2°;

k =2 donne i2' = + ou - 20,7°;

k =3 donne i3' = + ou - 32,1°;

k =4 donne i4' = + ou - 45,1°;

k =5 donne i1' = + ou - 62,2°;

source polychromatique :

pour i0 =0 ; a = 3,326 10-6 m ; k=2 ; l=400 10-9 m

sin i' = kl/a = 2* 400 10-9 / 3,326 10-6 = 0,240 soit i' = 13,91°.

pour i0 =0 ; a = 3,326 10-6 m ; k=2 ; l=780 10-9 m

sin i' = kl/a = 2* 780 10-9 / 3,326 10-6 = 0,469 soit i' = 28°.

calcul identique avec k=1 et les deux longueurs d'ondes extrèmes:

pour i0 =0 ; a = 3,326 10-6 m ; k=1 ;

sin i' = kl/a = 400 10-9 / 3,326 10-6 = 0,12 soit i' = 6,9°.

sin i' = kl/a = 780 10-9 / 3,326 10-6 = 0,234 soit i' = 13,5°.

pas de chevauchement de l'ordre 1 et de l'ordre 2.

calcul identique avec k=3 et les deux longueurs d'ondes extrèmes:

pour i0 =0 ; a = 3,326 10-6 m ; k=3 ;

sin i' = kl/a = 3*400 10-9 / 3,326 10-6 = 0,36 soit i' = 21,1°.

sin i' = kl/a = 3*780 10-9 / 3,326 10-6 = 0,703 soit i' = 44,7°.

chevauchement de l'ordre 2 et de l'ordre 3.


Les niveaux d'énergie de l'atome d'hydrogène sont donnés par la relation :

En = - A /n² où n est un nombre entier naturel non nul et A = 13,6 eV

  1. Définir l'énergie d'ionisation. Quelle est l'énergie d'ionisation de l'atome d'hydrogène en eV ?
  2. Un atome d'hydrogène passe de l'un quelconque des états excités tels que n >2, à l'état n = 2. Au cours de chaque transition possible, une radiation est émise, l'ensemble des radiations émises constituant la série de Balmer.
    - Montrer que la longueur d'onde l (en mètres) de l'une quelconque des radiations de cette série peut s'écrire sous la forme : 1/ l = RH ( 1/ 2² -1 /n²)
    - Expliciter RH en fonction de A, h et c. Calculer RH dans le système international.
    - Déterminer à quelle transition correspond la radiation (Ha) de la série de Balmer de longueur d'onde l 1 = 656 nm
    Données :

constante de Planck : h = 6,62 10-34 J.s ;

célérité de la lumière dans le vide : c = 3 108 m.s-1 ;

1 eV = 1,6 10-19 J.

corrigé

L'énergie d'ionisation est l' énergie nécessaire pour arracher l'électron de l'atome d'hydrogène : 13,6 eV.

énergie de l'électron au niveau n >2 : En = A/n²

énergie de l'électron au niveau n=2 : E2 = A / 2²

différence d'énergie : En - E2 = -A( 1/ n² - 1/ 2²)

cette différence d'énergie est égale à l'énergie du photon émis soit hc / l.

d'où hc / l = A( 1/ n² - 1/ 2²) et 1 / l = A/ (hc) ( 1/2²-1/ n² )

RH =A/ hc = 13,6 * 1,6 10-19 / (6,62 10-34 *3 108) = 1,08 107 .

l= 656 10-9 m

1 / 656 10-9 =1,52 106= 1,08 107(1/4 - 1/n²)

1/4 - 1/n² =0,14

1/n² = 0,25 - 0,14 =0,11

n²= 9,1 donc n =3.


à suivre ...
retour - menu
à bientôt ...