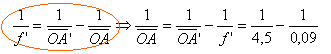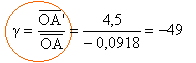|
projecteur de diapositives Antilles 09/00
|
||||||
|
||||||
|
|
Un projecteur de diapositives comprend une source lumineuse (S) placée entre un miroir concave et un condenseur, un support de diapositive et un objectif de distance focale convenable. principe de l'appareil : Cet appareil perment de projeter sur un écran une image agrandie de la diapositive : objet entierement transparent que l'on éclaire grâce à la source. Dans cette première partie l'objectif est assimilé à une lentille mince convergente de centre optique O et de distance focale f' =90 mm. La diapositive de format 24 mm * 36 mm constitue l'objet lumineux. Elle est centrée sur l'axe optique de la lentille et située dans un plan perpendiculaire à celui-ci. On note A l'intersection de la diapositive avec l'axe optique. 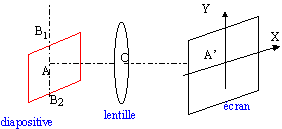
|
|||||
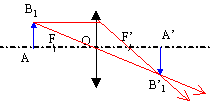
l'objet est réel ; l'image est réelle inversée par rapport à l'objet ; B'2 est symétrique de B'1 par rapport à A. formule de conjugaison : mesure algébrique de OA' = 4,5 m distance focale image f' = 0,09 m
d'où mesure algébrique de OA = -0,0918 m = -91,8 mm. ce résultat pouvait être prévu : 4,5 m est considéré comme l'infini par rapport à la distance focale 0,09 m. l'objet, dont l'image est rejetée à l'infini se trouve dans le plan focal objet. grandissement : les dimensions de l'image sont : 0,024*49 = 1,17 m et 0,036*49 = 1,76 m l'écran conseillé convient.
|
||||||
|