|
lunette astronomique .
|
||||||
|
||||||
|
|
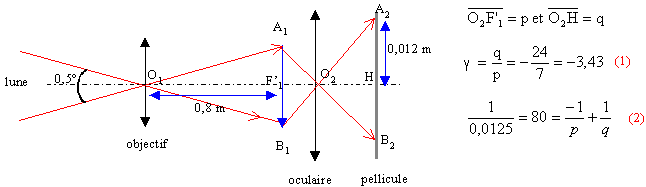
Une lunette astronomique est composée d'une lentille mince (utilisée comme objectif) de distance focale f'1=80 cm et d'un oculaire constitué d'une lentille mince convergente de distance focale f'2=1,25 cm. On place un boitier d'appareil photographique (sans objectif) derrière l'oculaire de la lunette, perpendiculaire ment à l'axe optique principal. L'instrument est dirigé vers la lune dont le diamètre apparent pour une observation à l'oeil nu est 30 minutes d'angle. La distance moyenne terre-lune est D=3,8 105 km.
|
|||||
|
30 minutes d'angle = 0,5 degré = 0,5*3,14/180 = 8,7 10-3 radian la lune (l'objet pout la première lentille) est à linfini : l'image A1B1 de la lune donnée par cette lentille est dans le plan focal image. 8,7 10-3 = A1B1 / 0,8 A1B1 = 7 mm
(1) donne le grandissement: celui ci est négatif car p <0 et q>0. (2) formule de conjugaison pour la seconde lentille. résoudre ce système de 2 équations : (1) donne p= -0,291 q (2) s'écrit : 80 = 3,43 / q + 1/q = 4,43 /q d'où q = 5,53 cm. la pellicule est à 5,53 cm de l'oculaire. le grandissement de la seconde lentille est toujours : |g |= 3,43 A2B2 = 10-5 m A1B1 = 10-5 /3,43 = 2,91 10-6 m distance terre lune : 3,8 10 8 m y : distance minimale de deux cratéres lunaires donnant deux images distinctes y / A1B1 = distance terre lune / distance focale première lentille (Thalès) y = 3,8 108 * 2,91 10-6 / 0,8 y = 1,38 km. sans accomoder : l'objet observé se trouve à l'infini. cet objet est l'image de la pellicule donnée par la loupe. la pellicule se trouve donc dans le plan focal objet de la loupe. puissance de la loupe : b / AB avec b pouvoir séparateur de l'oeil AB = 10-5 m puissance = 3 10-4 / 10-5= 30 dioptries.
|
||||||
|