Aurélie 10/02

coccinelle sur la troteuse d'une horloge

sel de Glauber


Google



 Soit une horloge dont la trotteuse des secondes a une longueur L = 70,0 cm. Sur cette trotteuse, partant de l'extrémité de l'aiguille, à t = 0 s, une coccinelle avance à vitesse constante Vc = 1,40 cm/s

  1. Calculer la vitesse angulaire w de rotation de l'aiguille autour de l'axe de rotation.
  2. Montrer que toutes les 5 s, l'aiguille s'est déplacée d'un angle de 30°.
    - Donner la relation existante entre q (angle), w et t.
  3. Calculer la distance parcourue d par la coccinelle sur l'aiguille en 5 s puis repérer les positions sur 1 schéma (réprésentant 1 cercle et la trotteuse tracée toutes les 5 s.
  4. Que dire du mouvement de la coccinelle :
    - dans le référentiel trotteuse ?
    - dans le référentiel terrestre ?
  5. On appelle Vtrot/terre la vitesse en un des points de la position de la coccinelle sur la trotteuse dans le référentiel horloge.
    - Calculer les valeurs des vitesses pour t = 25 s et t = 40 s
    - Représenter les vecteurs vitesses associés. les vecteurs sont écrits en bleu et en gras
    - Placer en ces points le vecteur Vc
  6. Calculer la valeur de la somme vectorielle V(t) = Vc + V trot/terre (t) aux instants t = 25 s et t = 40 s. Justifier.
  7. En utilisant la direction de Vc + V trot/terre (t)
    -Tracer le plus précisément possible la trajectoire correspondant au mouvement dans le référentiel terrestre.
    - Calculer V(t) vitesse de la coccinelle sur cette trajectoire aux instants t = 25 s et t = 40 s.
  8. Conclure en donnant la relation qu'il existe entre V(t), Vc, t et w.

 

corrigé
1 tour correspond à 2*3,14 = 6,28 rad parcourus en 60 secondes

w = 6,28/60 = 0,104 rad/s.

angle balayé en 5 secondes : q = w t = 0,104 *5 = 0,52 rad

0,52 *180 / 3,14 = 30°

la coccinelle parcourt 0,014*5 = 0,07 m sur l'aiguille toutes les 5 secondes

dans le référentiel de la troteuse la coccinelle a un mouvement rectiligne uniforme.

dans le réferentiel lié à la terre, la coccinelle décrit une spirale.

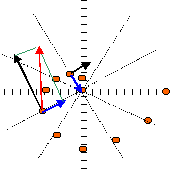
Vc en bleu dirigée vers le centre du cercle

Vtrot/ terre en noir perpendiculaire au rayon du cercle

V(t) en rouge tangent à la spirale, somme vectorielle des deux vitesses précédentes

en 25 s la coccinelle a parcouru : 0,35 m et se trouve à r = 0,35 m du centre du cercle

Vtrot/ terre = w r = 0,104*0,35 = 0,0364 m/ s.

en 40 s la coccinelle a parcouru : 0,56m et se trouve à r = 0,7-0,56 = 0,14 m du centre du cercle

Vtrot/ terre = w r = 0,104*0,14= 0,0145 m/s

Vc = 0,14 m/s

Vc et Vtrot/terre sont perpendiculaires

V(t) =Vc + V trot/terre = racine carrée (V²c + V² trot/terre)

rac carrée (0,14² + 0,0364² ) = 0,1446 m/s.

rac carrée (0,14² + 0,0145² ) = 0,141 m/s.

V²(t) = V²c + V²trot/ terre

V²(t) = V²c + (w r)² avec r = 0,7 - Vc t.  

Le sel de Glauber est utilisé dans les installations de chauffage solaire et dans les conditionneurs d'air. Le sel de Glauber est en fait du sulfate de sodium déca-hydraté.

  1. Donner la formule du sel de Glauber.
  2. On veut préparer 100mL de solution de ce sel de concentration en soluté apporté egale à 0,1 mol.L-1. Quelle masse de sel faut-il peser pour préparer cette solution ?
  3. Calculer la concentration des espèces ioniques contenues dans la solution après avoir ecrit l'équation de la réaction de dissolution.
  4. On ajoute à 50mL de cette solution, un volume de 2,5 cL de solution de chlorure de baryum de concentration 0,05 mol.L-1. Qu'observe-t-on ? Ecrire l'équation de la reaction qui se produit. Calculer la concentration en ions chlorure de la solution finale.

On donne: Na =23.0 ; S=32 ; O=16 ; H=1 ; Cl =35,5 ; Ba=137,3 g.mol-1

corrigé
Na2 SO4, 10 H2O

masse molaire : 46+96+180 = 322 g/ mol

0,01 mol dans 100 mL

322*0,01 = 3,22 g.

Na2 SO4 --> 2Na+ et SO42-.

[SO42-]= 0,1 mol/L ; [Na+]= 0,2 mol/L

Ba2+ + SO42- = BaSO4 (solide)

BaCl2(s) --> Ba2+ + 2 Cl-.

[Cl-]= 2* 0,05*25 / (50+25) = 0,0333 mol/L.

(2,5 cL = 25 mL ) 

à suivre ...
retour - menu
à bientôt ...