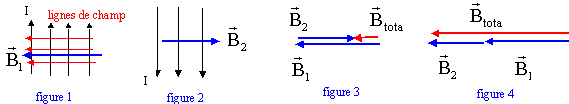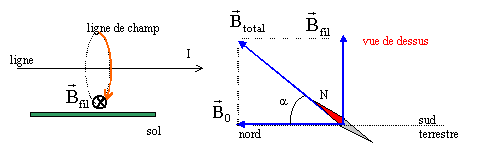|
superposition
de champs magnétiques
solénoïdes
|
|
|
|
Deux fils de cuivre verticaux sont
placés symétriquement de chaque coté d'une boussole horizontale. En
l'absence de courant dans les fils la boussole est orientée dans le
champ magnétique terestre dont la composante horizontale est B0=
2 10-5 T ( figure 1 : vue de dessus).
- Représenter le vecteur champ
magnétique au point M où se trouve la boussole en l'absence de courant.
- On fait circuler dans le fil de
gauche un courant I= 5 A. La boussole dévie de 50° ( figure 2
ci-dessous : vue de dessus).
- Déterminer le sens et la direction du champ crée par le courant au
point M.
- En déduire le sens du courant dans le conducteur.
- Quelle est la norme du champ crée par le courant.
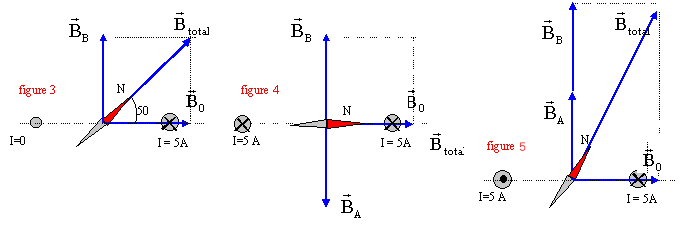
- Déterminer l'orientation prise par la
boussole dans chacun des cas suivant :
- On fait passer dans le fil B ( à droite) un courant de 5A drigé vers
le haut. I=0 dans le fil de gauche ( fil A)
- On fait passer dans chaque fil un courant de même intensité et de
même sens.
- On fait passer dans les fils des courants de même intensité mais de
sens contraire.
corrigé
|
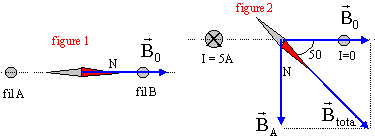
figure 1 : la boussole indique la direction et le sens du
champ magnétique terrestre noté B0.
figure 2 : la boussole s'oriente suivant le champ magnétique
total.
La boussole tourne de 50° dans le sens
des aiguilles d'une montre : le champ magnétique du courant est dirigé
vers le bas .
L'observateur d'Ampère couché sur le fil
vertical, regarde vers M ( le centre de la boussole), le courant entre
par ses pieds et sort par la tête ; son bras gauche tendu indique le
sens du courant : de haut en bas ( représenté par la croix dans le fil
n°1)
La norme du champ magnétique crée par le
courant est égale à :
tan 50 = BA / B0
d'où BA =B0 tan 50 = 2 10-5 * 1,19 = 2,38 10-5 T.
|
|
Un solénoïde S1
de longueur L= 0,5 m est alimenté par un courant continu d'intensité I=
3A.
- Représenter le
solénoïde sur un schéma et tracer quelques lignes de champ. Indiquer le
sens du courant et l'orientation des lignes de champ.
- La valeur du champ à l'intérieur de la bobine longue est 4,5 mT. Quel
est le nombre de spires ?
- On place S1
à l'intérieur d'un second solénoïde de même longueur, de même exe et
alimenté par un courant de même intensité. Le sens du champ à
l'intérieur de S1 est le même que précédemment, mais sa valeur n'est
plus que 1,5 mT.
- Quelle sont les caractéristiques du champ crée par S2 ?
- Combien S2 comporte t-il de spires ?
- Quelle sera la valeur du champ dans S1 si on inverse le
sens du courant dans S2 ?
corrigé
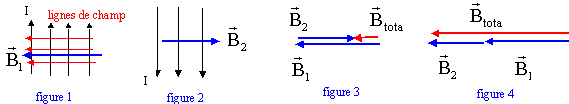
figure 1 : solénoïde S1 seul
.
B1 = m0 nI avec m0 = 4 p 10-7
; I= 3A et B1 = 4,5 10-3 T
n = 4,5 10-3
/ ( 4 p 10-7 *3) = 1194
spires par mètre
soit 1194*0,5 = 597 spires ( pour une longueur de 50 cm)
figure 2 : solénoïde S2 seul .
figure 3 : solénoïdes S1 et S2
( courants de sens contraire)
Le champ total
dans S1 a diminué donc le second solénoïde crée un champ de
sens contraire
B2 =
3 10-3 T
B2 = m0 n2I avec m0 = 4 p 10-7
; I= 3A et B2 = 3 10-3 T
n2 =
3 10-3 / ( 4 p 10-7 *3) = 796
spires par mètre
soit 796*0,5 = 398 spires ( pour une longueur de 50 cm)
figure 4 : solénoïdes S1 et S2(
courants de même sens)
Le courant change
de sens dans S2 ; donc le champ magnétique B2
change de sens
Btotal = 4,5+3 = 7,5 mT.
|
|
- Parmi les dispositifs suivants, lesquels sont sources de
champ magnétique : a- un fil de cuivre ; b- un fil de cuivre parcouru
par un courant ; c la Terre ; d- un morceau de plastique frotté.
- L'expérience qui suit est destinée à mesurer la valeur BH
de la composante horizontale du champ magnétique terrestre : une
aiguille aimantée posée horizontalement face à un cadran gradué en
degrés d'angles, est placée à l'intérieur du solénoïde convenablement
orienté pour qu'en l'absence de courant, elle s'oriente
perpendiculairement à l'axe du solénoïde, face à la graduation zéro. A
quel champ magnétique son orientation est-elle due ?
- Lorsqu'un courant circule, elle tourne d'un angle a par rapport à cette position. On repère les
différentes valeurs de l'angle a pour
différentes valeurs de I. Les résultats sont les suivants :
|
I (mA)
|
4
|
8
|
12
|
16
|
20
|
|
angle a °
|
26
|
45
|
56
|
63
|
68
|
|
tan a
|
0,49
|
1
|
1,5
|
2
|
2,5
|
Tracer le graphe I = f(tan a) ; en déduire
la relation entre I et tan a.
- Schématiser ci-contre les champs magnétiques qui agissent
sur l'aiguille déviée d'un angle a.
- Donner la relation entre la tangente de l'angle a et les valeurs des champs magnétiques qui
agissent sur l'aiguille.
- Exprimer BH la composante horizontale du champ
magnétique terrestre en fonction de tan a
et I et calculer sa valeur. Données : µ0 = 4p.10-7 u SI ; : N = 800 spires ; L =
40 cm
corrigé
sources de champ
magnétique : un fil de cuivre parcouru par un courant ; la Terre.
en l'absence de courant dans le solénoïde, l'aiguille
aimantéeest soumise à l'action du champ magnétique terrestre.
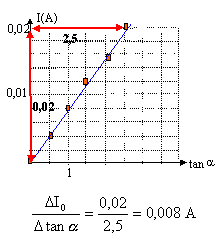
I (A) = 0,008 tan a.
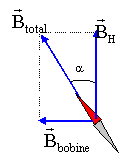
tan a = Bbobine / BH
; BH= Bbobine /tan a
= 8 10-3Bbobine / I
Or Bbobine = m0
NI/L ; BH= 8 10-3m0
N/L
BH= 8 10-3 * 4 *3,14 10-7
*800 / 0,4 = 2 10-5 T.
|
|
Le fil de la ligne d'alimentation d'un tramway est situé à 6,0
m au-dessus du sol. Dans ce fil, orienté dans le sens nord-sud, passe
un courant d'intensité I= 150 A dans la direction nord-sud. Ce courant
produit un champ magnétique.
- Comment sont les lignes de champ autour du fil ?
- Décrire ce champ magnétique au niveau du sol et dans le
plan vertical passant par le fil. Faire un schéma.
- À la distance r du fil, la valeur de ce champ magnétique
est donné par la relation : Bfil= 2p
10-7 I/r
- Calculer la valeur de Bfil et la comparer à celle de la
composante horizontale du champ terrestre ( B0=2 10-5 T).
- Schématiser le champ résultant en un point du sol et calculer sa
valeur.
corrigé
les lignes de champs
sont des cercles concentriques, centrés sur le fil
le champ magnétique est tangent à la ligne de champ au point
considéré ; son sens est donné par la règle de l'observateur d'Ampère.
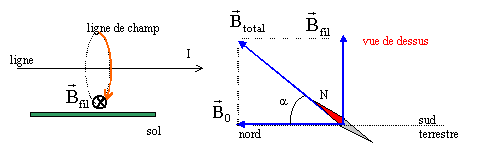
Bfil= 2p 10-7
I/r = 6,28 10-7*150/6 = 1,57 10-5 T, du même
ordre de grandeur que la valeur du champ terrestre.
Btotal = [B²fil + B²0]½=
[1,57² + 2²]½ 10-5= 2,54 10-5 T
|
|
|