|
|
||||||
|
||||||
|
|
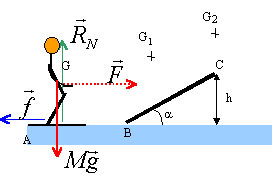 On étudie le mouvement du centre d'inertie du skieur. Sur le
trajet AB la force de traction F est constante et les forces de
frottements sont équivalents à une force f constante, colinéaire à la
vitesse mais de sens contraire, de norme f = 100 N. Au delà de B sur le
tremplin et lors du saut les frottements sont négligeables. g =10 m/s² ; AB =200 m; h= 2m.
|
|||||
|
travail de la force motrice F sur le parcours AB : W(F)A-->B = F* AB = 200 F. travail de la force de frottement f sur le parcours AB : W(f)A-->B = f* AB cos 180 = -f AB = -100* 200 = - 2 104 J. somme des travaux des forces :( F-f) AB = (F-100)*200 J variation de l'énergie cinétique sur le parcours AB : état initial A : pas de vitesse donc Ec(A) =0 Etat " passage en B " : vitesse Vb et Ec(B) = ½mv2B variation énergie cinétique = énergie cinétique finale - énergie cinétique départ D Ec = ½ mv2B - 0 = ½ mv2B la variation de l'énergie cinétique est égale à la somme des travaux des forces : ½ mv2B = (F-f) AB
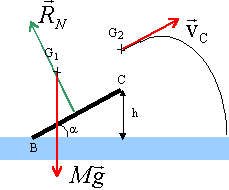
Lors du parcours BC, seul le poids travaille (RN perpendiculaire à la vitesse ne travaille pas). W(P)B-->C = mg (Hb-Hc) = - mgh (travail résistant du poids quand on monte) B est prise comme origine des altitudes et Hc = h variation de l'énergie cinétique sur le parcours BC : état initial B : vitesse vB et Ec(B) = ½mv2B Etat " passage en C " : vitesse vC et Ec(C) = ½mv2C variation énergie cinétique = énergie cinétique finale - énergie cinétique départ D Ec = ½ mv2C - ½ mv2B la variation de l'énergie cinétique est égale à la somme des travaux des forces : ½ mv2C - ½ mv2B = -mgh. remplacer ½ mv2B par ( F-f) AB ½ mv2C - ( F-f) AB = -mgh. ½ mv2C + mgh = ( F-f) AB m / AB [½ v2C + gh] + f = F application numérique : vC = 72 / 3,6 = 20 m.s-1. F = 100 + 80 / 200 ( 0,5*20*20+10*2) = 188N. Le mouvement du skieur après le saut : Le skieur est soumis uniquement à son poids : le mouvement est un mouvement de chute libre avec vitesse initiale La trajectoire est un arc de parabole. Le vecteur vecteur initiale est parallèle au plan incliné et sa norme est 20 m/s. seule la composante verticale de la vitesse est modifiée lors de la chute libre( composante de la vitesse suivant la direction du poids, seule force qui agit ) la composante horizontale de la vitesse n'est pas modifiée : au sommet de la parabole, le vecteur vitesse est horizontale. Sa composante verticale est nulle; sa composante horizontale est : 20 cos a. |
||||||
|
Les communications télévisuelles et vocales comme le téléphone sont aujourd'hui transmises par l'intermédiaire de satellites en orbite circulaire autour de la terre. On utilise aussi bien des satellites géostationnaires qui circulent à l'altitude h=36000 km dans le plan équatorial en restant à la vertical d'un même point de la terre, que des satellites de basse altitude h'=10352 km et de période T'=6,00 h .
données : rayon terrestre: R=6380 km période de rotation de la terre sur elle même T=86164 s corrigé Un satellite géostationaire paraît fixe pour un observateur terrestre, car il tourne dans le plan équatorial, dans le même sens que la terre, avec la même vitesse angulaire ( donc la même période) : période 86140 s. h altitude : R+ h = = 6,38 106 + 3,6 107 =4,24 107 m circonférence de l'orbite : 2p(R+h) =2*3,14*4,24 1 107 =2,66 108 m vitesse du satellite (m/ s ) = distance (m) / période (s) : v = 2,66 108 / 86164 = 3090 m/s énergie cinétique
0,5 * 500*3090² = 2,39
109 J.
h altitude : R+h' = = 6,38 106 + 1,0352 107 =1,67 107 m circonférence : 2*3,14*1,67 107 =1,05 108 m période : 6*3600 = 21600 s vitesse = 1,05 108 / 21600= 4861m/s énergie cinétique :0,5 * 500*4861²= 5,9 109 J. |
||||||
|