Aurélie 01/02

énergie mécanique, travail d'une force

bille de flipper

divers mouvements


Google



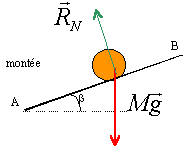
Le lanceur d'un " flipper " est constitué d'un ressort et d'une tirette qui permet de comprimer le ressort. Une bille de masse m = 95 g vient se positionner contre une butée solidaire de la tirette. Quand la bille est projetée par le lanceur, elle aborde un plan incliné d'un angle b = 21° par rapport à Phorizontal , selon une ligne de plus grande pente.

Afin d'étudier le mouvement de la bille, on la schérnatise par un petit bloc glissant en translation sur le plan incliné.

  1. Le joueur lâche la tirette ; pendant la détente du ressort, le bloc reste au contact de la butée.
    - Faire une analyse des forces qui s'exercent sur le bloc et des travaux travaux effectués par ces forces.
    - Le bloc est expulsé avec une vitesse v = 3, 1 rn/s. Calculer le travail de la résultante des forces au cours de cette phase. Quel travail peut-on négliger ?
  2. Le bloc aborde le plan incliné.
    - Déterminer la longueur L qu'il est susceptible de parcourir sur le plan avant qu'il ne redescende.
    - En fait, il ne parcourt qu'une distance de 1,1 m. Calculer le travail des forces de frottement au cours de ce parcours.
  3. Arrivé au sommet de la trajectoire, il redescend ,en admettant que le travail des frottements reste le même, calculer la vitesse du bloc au bas du plan.

 
corrigé
bille en contact avec le ressort :

si les frottement sont négligeables la bille est soumise à :

son poids, vertical vers le bas ; à l'action du plan perpendiculaire au plan et à l'action de la butée vers le haut parallèle au plan

théorème de l'énergie cinétique :

l'action du plan et le poids perpendiculaire à la vitesse ne travaillent pas sur le plan horizontal

au cours du déplacement AB travail de la force exercée par la butée : cette force n'est pas constante, le calcul du travail n'est pas possible en première.

écrire que la variation d'énergie cinétique est égal au travail de la résultante des forces :

vitesse initiale nulle donc ½mv²départ =0

DEc = ½mv²fin

la masse s'exprime en kg : 95 g = 0,095 kg

0,5 * 0,095 *3,1 ² = 0,456 J.

 


sur le plan incliné :

sur le plan incliné la bille est soumise à l'action du plan (perpendiculaire au plan si pas de frottement) et à son poids :

travail du poids au cours du déplacement AB = L : mg(HA-HB)

avec HA = 0 origine des altitudes et HB = Lsinb ;

W(poids) A-->B = -mgLsinb

l'action du plan perpendiculaire au plan ne travaille pas.

variation d'énergie cinétique = travail du poids

DEc = ½mv²B - ½mv²A = -mgLsinb

L = (v²A -v²B ) / (2gsinb) = 3,1² / (2*9,8 sin 21) =1,37 m.

en tenant compte des frottements :

variation d'énergie cinétique = travail du poids + travail des frottements

½mv²B - ½mv²A = -mgLsinb +Wf

Wf = m[gLsinb -½v²A ]

Wf = 0,095[9,8*1,1*sin21-0,5*3,1²]= -0,089 J.

descente avec frottements :

variation d'énergie cinétique = travail du poids + travail des frottements

le travail du poids est moteur en descente : mg AC sinb avec AC =1,1 m

la vitesse initiale en C est nulle ( haut du plan)

½mv²C - ½mv²A = mg AC sinb +Wf = 0,367 - 0,089 = 0,278 J

v²A = 2[g AC sinb +Wf / m ]

v²A =2[9,8*1,1*sin21 -0,089 / 0,095]= 5,85

vA = 2,41 m/s.


 

  1. Observer les figures ci-contre. Pour chaque cas, préciser si le solide S est pseudo-isolé ou non en justifiant
  2. Deux pierres de masses identiques sont lancées du haut d'une falaise : l'une est lancée vers le haut, l'autre vers le bas. Comparer le travail du poids de chaque pierre, au cours de leur chute jusqu'au sol supposé horizontal ; justifier.
  3. Le plan est rugueux, les frottements peuvent être assimilés à une force de valeur f constante. le solide est lâché en I à la vitesse Vi et parcourt la distance IJ.
    - Déterminer sa vitesse lorsqu'il arrive en J

    Données : m = 100 g ; g = 9,8 N.kg-1. Vi = 4,4 m.s-1 ; f = 0,50 N ; IJ =d = 2,0 m ; b = 20°.

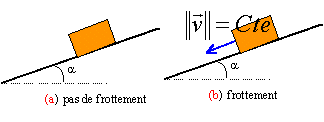
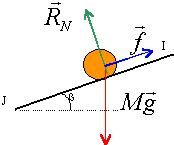
corrigé

a : le bloc descend le plan et sa vitesse augmente en absence de frottement ; la somme vectorielle des forces n'est pas nulle et le solide n'est pas pseudo isolé.

b : mouvement rectiligne uniforme (norme de la vitesse constante) donc solide pseudo isolé d'après le principe d'inertie.

Le travail d'une force constante comme le poids ne dépend pas du chemin suivi mais uniquement des positions de départ et d'arrivée.

le travail du poids est identique si les pierres sont la même masse.

descente avec frottements :

écrire que la variation d'énergie cinétique est égal au travail de la résultante des forces :

l'action du plan perpendiculaire à la vitesse ne travaille pas.

variation d'énergie cinétique = travail du poids + travail des frottements

le travail du poids est moteur en descente de I en J: mg IJ sinb

travail des frottements = - f IJ

½mv²J - ½mv²I = mg IJ sinb - f IJ

v²J = v²I + 2 IJ (g sinb -f / m)

v²J = 4,4² + 2*2(9,8 sin20 -0,5 /0,1) = 12,76

vJ = 3,57 m/s.

à suivre ...
retour - menu
à bientôt ...