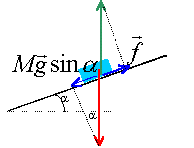Aurélie nov 2001

forces- première S

disque de meule

les pyramides

poussée d'Archimède


Google



Un disque de meule est en rotation autour d'un axe. L'un de ces points décrit une trajectoire circulaire de rayon r = 5 cm. La vitesse angulaire w = 4,7 rad/s.

  1. Représenter à l'échelle la trajectoire de ce point.
  2. Exprimer la fréquence de rotation en tours / min.
  3. Calculer la vitesse du point mobile en un point de sa trajectoire.
  4. Représenter le vecteur vitesse instantané à 2 instants différents. ( 1cm pour 0,1 m/s).
corrigé

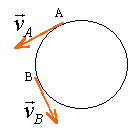
un tour correspond à 2*3,14 = 6,28 rad

4,7 / 6,28 = 0,748 tours /s.

0,748*60 = 44,9 tours /min.

vitesse linéaire : v = w r avec r=0,05 m

v = 4,7 *0,05 = 0,235 m/s.

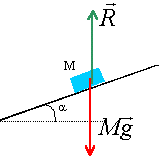
Pour construire les pyramides les égyptiens ont sans doute utilisé la technique du plan incliné. On prend pour l'inclinaison du plan a =15° et g =9,8 N/kg.

  1. Un bloc de pierre cubique de 1 m de côté a une masse de 2500 kg.
    - Calculer son poids.
    - Combien d'hommes exerçant chacun une force de 800N serait nécessaire pour le soulever. Est-ce possible ?
  2. On imagine le bloc de pierre immobile sur le plan incliné.
    - Quelles sont les forces qui agissent sur lui ? faire un schéma ( 1cm pour 10 000 N )
    - Calculer la force de frottement f qui agit sur le bloc.
  3. Des rouleaux intercalés entre le bloc de pierre et le sol rendent les frottements négligeables. Pour maintenit le bloc en équilibre on exerce une force F parallèle au plan dirigée vers le haut.
    - Représenter les différentes forces appliquées au bloc.
    - Projeter le poids sur la ligne de plus grande pente ; quelle est la valeur de cette composante ?
    - Quelle doit être la valeur minimale de la force F pour que le bloc monte le plan incliné ?
    - Combien d'hommes faut-il utiliser ?
corrigé

poids (N) = masse (kg) *9,8 = 2500*9,8 = 24 500 N.

24500 / 800 = 31 hommes.

solide immobile : la somme des forces agissant sur le bloc est nulle

poids et action du plan sont opposées

projections de ces forces sur un axe parallèle au plan dirigé vers le haut

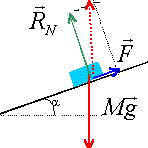
f = mg sin a = 2500*9,8 sin15 = 6341 N.

le bloc est soumis à l'action des rouleaux, perpendiculaire au plan, au poids et à la force musculaire F.

F= 6341 N

6341 / 800 = 8 hommes sont nécessaires.

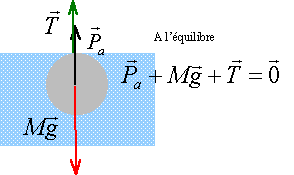
On considère une boule d'aluminium sphérique de diamètre d=40 mm et de masse volumique r = 2,7 g/cm3.

  1. Quel est le poids de cette boule à l'altitude zéro (g=9,8 N/kg) ?
  2. Quelle est la valeur de la poussée d'Archimède exercée sur cette boule ( masse volumique de l'air 1,293 g/L) ?
  3. Quelle est la valeur de la poussée d'Archimède exercée sur la boule immergée dans l'eau ?
    - Comparer ces trois valeurs ?
  4. La boule est accrochée à l'extrémité d'un ressort vertical (k=0,5 N/m).
    - Représenter les forces agissant sur la boule.
    - Quel est l'allongement du ressort ?
  5. Même question la boule est immergée dans l'eau.
corrigé

volume de la boule sphérique : 4/3 p r3 avec r = 20 mm = 2 cm

V = 4/3*3,14 *23 = 33,5 cm3

masse (g) = 33,5 * 2,7 = 90,45 g = 0,09 kg.

poids : 0,09*9,8 = 0,882 N.

poussée d'Archimède due à l'air = poids du volume d'air V

masse volumique air : 1,293 kg/ m3.

volume : : 33,5 cm3 = 33,5 10-6 m3.

poussée : 1,293*9,8*33,5 10-6 = 4,2 10-4 N.

négligeable devant le poids.

poussée d'Archimède due à l'eau = poids du volume d'eau V

masse volumique eau : 1000 kg/ m3.

volume : : 33,5 cm3 = 33,5 10-6 m3.

poussée : 1000*9,8*33,5 10-6 = 0,328 N.

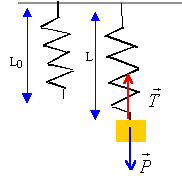
à l'équilibre tension et poids sont opposée

tension (N) = raideur (N/m) fois déformation du ressort (m)

mg = k(L-L0)

L-L0= mg / k = 0,88 / 0,5 = 1,76 m.

dans l'eau le poids paraît plus petit : 0,88 -0,328 = 0,552 N

nouvelle déformation : 0,552 / 0,5 = 1,10 m.

 

à suivre ...
retour - menu
à bientôt ...