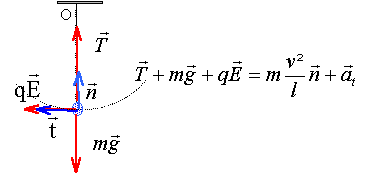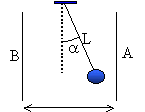
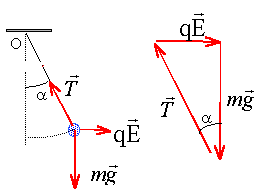
Aurélie déc 2001
pendule électrostatique

 

Web

www.chimix.com

Entre deux plateaux métalliques plans, parallèles, verticaux, équidistants de d=25 cm, on établit une tension UAB=U. Une sphère métallique de masse m=2g que l'on considérera comme ponctuelle est suspendue au bout d'un fil de masse négligeable de longueur L=25 cm.. Quand U=0, la sphère est équidistante des deux plateaux. On prendra g=10 m/s².

 

La charge de la sphère est q= -0,577 mC. On fait croître lentement U à partir de zéro.

La sphère est soumise à :

son poids, vertical vers le bas, norme mg = 2 10-3 *10 = 0,02 N

la force électrique, horizontale , à droite , norme |q|E avec E = |U| / d et d=0,25 m

la tension du fil dirigée suivant le fil

A l'équilibre la somme vectorielle de ces trois forces est nulle.

tan a =|q| U/(d m g).

Etablissons une relation entre a, d, m, |q|, U et g pour une position d'équilibre de la sphère.

U = d m g tan a / |q|

La sphère touche l'un des plateaux pour a =30°. Je calcule la valeur de U correspondante.

d = 0,25 m ; m = 2 10-3 kg ; g =10 m/s² ; |q| = 0,577 10-6 C ; tan 30 = 0,577 .

U = 0,25*2 10-3*10 * 0,577 / 0,577 10-6 = 5000 V

La sphère repart sans vitesse de la plaque qu'elle vient de toucher avec une charge q'= 2 m C. La tension vaut alors 500V. Calcul de la vitesse d'arrivée sur le plateau opposé.

appliquer le théorème de l'énergie cinétique entre le plateau A (départ) et le plateau B ( but)

la tension du fil, perpendiculaire à la vitesse ne travaille pas.

l'altitude de départ est égale à l'altitude finale ( la sphére est équidistante de A et de B si U=0), donc le poids ne travaille pas.

travail de la force électrique : q(VA- VB) = q UAB.

l'énergie cinétique initiale étant nulle, la variation d'énergie cinétique est égale à l'énergie cinétique finale :

½ m v² = q UAB soit v² = 2 q UAB / m

avec U= 500 V ; m = 2 10-3 kg et q = 2 10-6 C.

v² = 4 10-6 * 500 / 2 10-3 = 1 et v = 1 m/s.

 

 

La sphère partant dans des conditions identiques à la question précédente, on s'intéresse à son passage dans le plan vertical équidistant des 2 plateaux :
Schéma des forces appliquées à la sphère :

accélération :

dans la base de Frenet :

suivant l'axe n : -mg +T = maN= m v² / l

aN= v² / l avec l * = 0,25 m donc aN= 4 v².

il faut déterminer cette vitesse :

calcul identique à celui de la question précédente avec UAO = 250V ( la sphère est à égale distance des plaques soumises à la tension de 500 V)

v² = 2 q UAO / m

m = 2 10-3 kg et q = 2 10-6 C.

v² = 4 10-6 * 250 / 2 10-3 = 0,5 et v = 0,707 m/s.  

puis aN = 0,5 / 0,25 = 2 m/s².

 suivant l'axe t : qE= m at.

E = 500 / 0,25 = 2000 V/m.

at = 2 10-6 *2000 / 2 10-3 = 2 m/s².

retour - menu