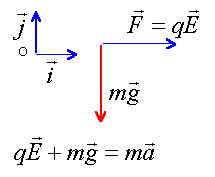|
||
|
Une petite sphère ( supposée ponctuelle) électrisée de masse m et portant une charge positive q telle que q/m = 10-6Ckg-1 est placée entre deux plaques métalliques A et B verticales distantes de d=4 cm. Ces deux plaques soumises à une tension positive UAB= U créent un champ électrique supposé uniforme. A la date t=0, la sphère est abandonnée sans vitesse initiale en un point M0 de coordonnées x0=d/2 et y0=L=1m. Soit g=10 m/s², intensité du champ de pesanteur. 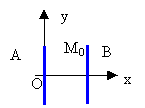
la tension UAB étant positive le champ électrique E pointe vers B, le plus petit potentiel. les vecteurs sont écrits en bleu et en gras.
composantes de l'accélération dans le repère O i j : a ( qE/m ; -g) la vitesse initiale est nulle ; position initiale OM0 (½d ; 1) la vitesse est une primitive de l'accélération : v ( qE/m t ; -gt) le vecteur position est une primitive du vecteur vitesse OM ( x= qE/(2m) t² +½d ; y = -½g t² + 1 ) éliminer le temps entre ces deux expressions pour trouver la trajectoire : t² = (1-y) 2 /g x = qE/(2m) (1-y)2 /g + 0,02 x = qE/(mg) (1-y) + 0,02 1-y = (x-0,02) mg / (qE) y = (0,02-x)mg / (qE) +1 équation d'une droite : la trajectoire est une droite. passer aux valeurs numériques : m /q = 106 et g=10 y = (0,02-x)107/E +1
0 = -½g t² + 1 soit : t²= 0,2 et t = 0,447 s. Valeur à donner à U pour que la trajectoire de la sphère passe par le point P de coordonnées (d ;0). 0 = (0,02-0,04)107/E +1 E = 2 105 V/m or E = U / d soit U = Ed = 2 105 *0,04 = 8000 V. |
||
|
retour - menu |