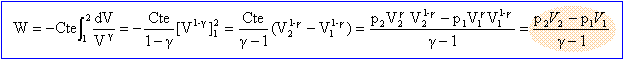|
|
||
|
||
|
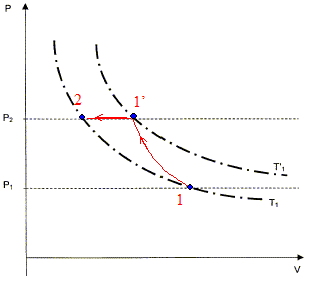
On veut comprimer une mole de gaz supposé parfait de l'étatinitial noté 1 caractérisé par (V1, P1= 105 Pa, T1=298 K ) vers un état final noté 2 caractérisé par (V2, P2= 2 105 Pa, T2). Cette compression est réalisée en deux étapes : - Une compression adiabatique qui amène le gaz dans un état intermédiaire noté 1' caractérisé par (V'1, P2, T'1 ). - Un refroidissement isobare pour obtenir l'état 2 caractérisé par (V2, P2= 2 105 Pa, T1).
Calcul de V1 : V1 = RT1/P1 =8,31*298/105 =2,48 10-2 m3 =24,8 L / mol.
calcul de V'1 et T'1 : transformation adiabatique : P1V1g = P2V'1g ; V'1g = P1/ P2 V1g ; V'1 = ( P1/ P2 ) 1/g V1 V'1 =(0,5)1/1,4 24,8 = 15,1 L/mol. équation des gaz parfaits : T'1 = V'1 P2 /R = 15,1 10-3*2 105 /8,31= 364 K.
On veut mesurer les travaux reçus W1, W2 et Wt correspondant successivement à la transformation adiabatique, le refroidissement isobare et à la transformation totale. travail élémentaire des forces de pression -pdV avec p= Cte / Vg intégrer entre V1 et V2.
pression en pascal, volume en m3. W1 = 8,31(364-298) / 0,4
=1,37 kJ. transformation isobare : dW2 = -P2dV ; W2 = -P2( V2 - V'1 ); or P2V2 = RT2= RT1 et P2V'1 = RT'1 d'où W2 = R( T'1-T1) W2 = 8,31(364-298) = 0,55 kJ. Wt = W1 + W2 = 1,92 kJ. On veut maintenant mesurer les échanges de chaleur Q1, Q2 et Qt Q1 = 0 car la compression est adiabatique. Q2 = Cp, m ( T1-T'1) = gR / (g-1)( T1-T'1)=1,4*8,31/0,4(298-364) = -1,92 kJ. Qt = Q2 = -1,92 kJ. Variation d'énegie interne DU = Wt + Qt = 0 La variation d'énergie interne d'un gaz parfait ne dépend que de la température finale et de la température initiale. Or ici la température initiale est égale à la température finale, d'où DU =0.
|
||
|
|